CUDA编程入门与性能优化：从线程组织到内存层级与并行加速

这篇笔记从 CUDA 入门出发，按“能跑→能查错→能计时→能优化”的路径系统讲清 GPU 线程组织、编译与工具链、内存层级与占有率，并以带宽/算术强度/并行规模为主线，用矩阵转置、归约、原子操作、warp 原语、共享内存与 bank 冲突、stream 与异步拷贝等案例串起一套可复用的性能分析与优化方法，帮助把程序从“正确”推到“更快”。

参考：《CUDA编程：基础与实战》

GPU硬件与CUDA程序开发工具
CUDA中的线程组织
简单CUDA程序的基本框架
CUDA程序的错误检测
获得GPU加速的关键
CUDA的内存组织
全局内存的合理使用
共享内存的合理使用
原子函数的合理使用
线程束基本函数与协作组
CUDA流（Streams）
使用统一内存编程（Unified Memory）
CUDA标准库的使用

1. GPU硬件与CUDA程序开发工具

1.1 计算能力（compute capability）：

计算能力（compute capability）是 NVIDIA 用来标识某款 GPU 所支持的 CUDA 硬件/指令特性的一套版本号，用于描述“支持哪些特性”，而不是直接描述“有多快”。版本号通常写作 X.Y：

X（主版本号）：通常对应一代核心架构（或一代架构能力集合）。
Y（次版本号）：同一主版本内的细分差异与小改进。

注意：计算能力 ≠ 计算性能。真实性能还会受到 CUDA 核心数、频率、显存带宽、缓存结构、功耗/温度限制等多因素影响。

1.2 表征计算性能的参数：

1.2.1 浮点运算峰值（FLOPS）

表示每秒最多可完成多少次浮点运算。GPU 常见量级为 FLOPS（TFLOPS）。峰值通常区分：

单精度（FP32）
双精度（FP64）

一般经验规律：

Tesla 系列：双精度峰值通常约为单精度的 1/2（部分型号约 1/3）。
GeForce 系列：双精度峰值通常只有单精度的 1/32 左右。

1.2.2. 显存带宽与显存容量

显存带宽（memory bandwidth）：对大量访存的任务会显著影响性能。
显存容量：决定问题规模能否放得下、程序能否运行。

1.3 CUDA给程序员提供两层API：

CUDA Driver API（驱动 API）：
- 更底层、控制更细、灵活性更高
- 编程复杂度更高
- 部分场景下是必须的
CUDA Runtime API（运行时 API）：
- 建立在 Driver API 之上
- 更常用、接口更易用、可读性更好

性能上两者几乎无差异。一般推荐优先使用 Runtime API，除非需求必须落到 Driver API 层面。

1.4 CUDA程序从CPU到GPU的调用层级

CPU 端程序通过 CUDA API/库将任务交给驱动，最终由驱动调度 GPU 执行：
应用程序（CPU端）：流程控制（读数据、分配内存、发起计算、收结果）。
CUDA库（可选）：如 cuBLAS、cuDNN 等高层封装库。
CUDA Runtime API：如 cudaMalloc、cudaMemcpy、kernel<<<>>>。
CUDA Driver API：负责与驱动交互，Runtime API很多实现也依赖它。
GPU：实际执行并行计算的硬件。

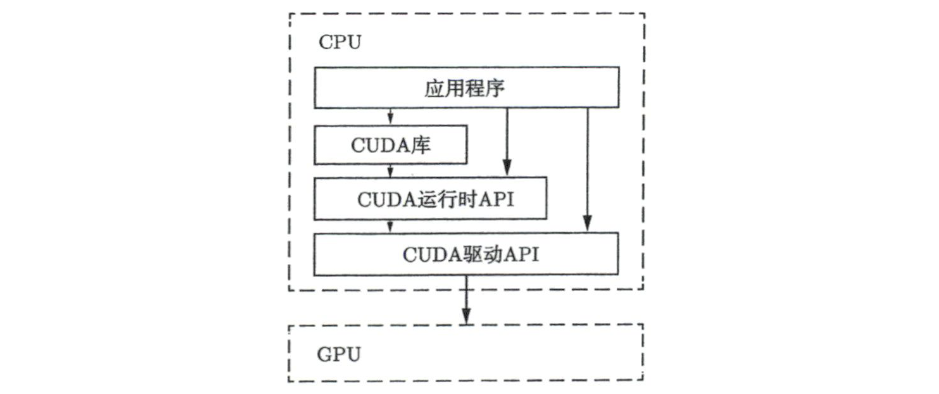
图里的箭头表达的是应用程序可以直接调用 Runtime API，也可以通过CUDA库间接调用；而Runtime API会再往下依赖Driver API，最终由Driver API去驱动GPU干活。

1.5 nvidia-smi程序检查与设置设备

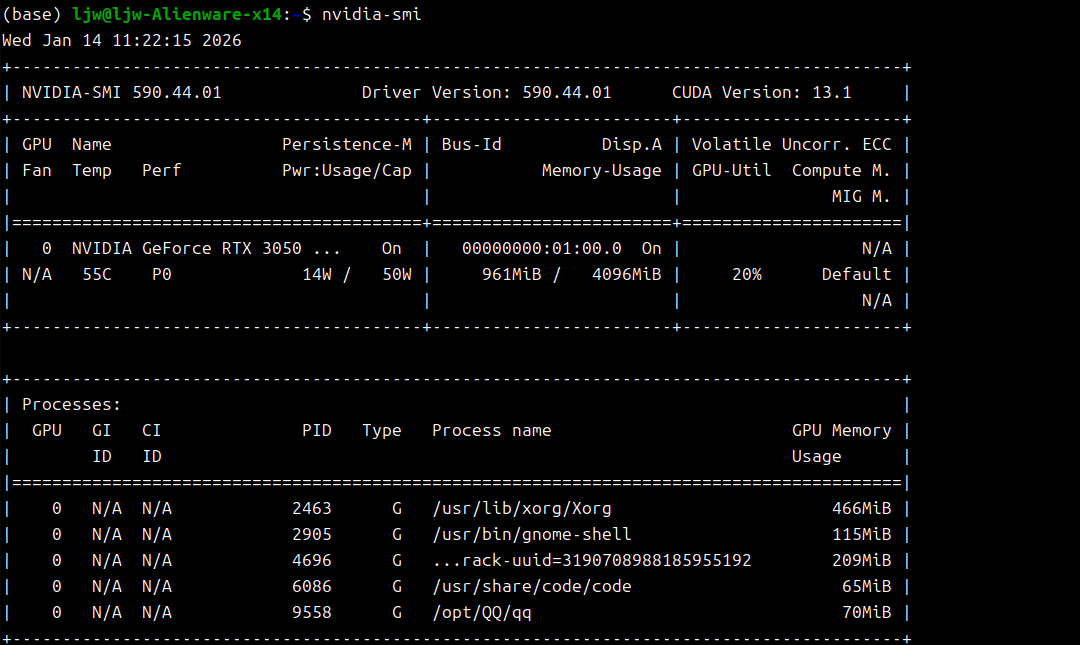
1.6 参考资料（官方文档与指南）

CUDA 官方文档入口：https://docs.nvidia.com/cuda/
编程指南（Programming Guides）
- CUDA C++ Programming Guide：https://docs.nvidia.com/cuda/cuda-c-programming-guide
- CUDA C++ Best Practices Guide：https://docs.nvidia.com/cuda/cuda-c-best-practices-guide
各架构优化指南（Tuning Guides）
CUDA API References
- CUDA Runtime API：https://docs.nvidia.com/cuda/cuda-runtime-api
- CUDA Driver API：https://docs.nvidia.com/cuda/cuda-driver-api
- CUDA Math API：https://docs.nvidia.com/cuda/cuda-math-api

2. CUDA中的线程组织

2.1 nvcc 与 .cu 源文件

nvcc 既可编译 CUDA 代码，也能编译纯 C++。典型 CUDA 程序通常包含：

主机端（CPU）代码：基本完整 C++
设备端（GPU）代码：CUDA 扩展 + 设备端受限的 C++

nvcc 会将主机端代码交给系统 C++ 编译器（如 g++/cl），自己负责编译设备端代码。CUDA 源文件扩展名为 .cu：

1	nvcc hello1.cu

2.2 CUDA 核函数（Kernel）

核函数必须满足以下约束：

使用 __ global__ 修饰。
返回类型必须为 void。
不支持可变参数列表（参数个数必须固定）。
必须通过三尖括号执行配置启动：kernel<<<grid, block>>>(…)。

三尖括号执行配置（Execution Configuration）：

grid size：线程块（block）的数量（网格中 block 的数量）
block size：每个 block 中的线程（thread）数量
总线程数：grid size × block size

核函数启动后通常是异步的。调试或需要强制同步时，可在主机端调用：

cudaDeviceSynchronize()：同步 CPU 与 GPU（常用于等待核函数完成，确保 printf 输出被刷新）。

其他要点：

不使用统一内存时，传给核函数的数组/指针必须指向设备内存（显存）。
核函数不能作为类成员函数；常见做法是在类成员里写“包装函数”调用 kernel。
无论从主机还是设备发起调用，核函数都在 GPU 上执行；调用时必须写 <<<…>>> 执行配置。

2.3 线程与索引：一维网格/线程块

从 Kepler 架构开始：

每个 block 最大线程数 block size = 1024
一维网格下最大 grid size ≈ 个block

核函数中每个线程都有唯一身份，可通过内建变量获得启动参数：

gridDim.x：网格在 x 方向的 block 数（≈ grid_size）
blockDim.x：每个 block 的线程数（≈ block_size）
blockIdx.x：当前线程所在的 block 编号，范围 [0, gridDim.x-1]
threadIdx.x：当前线程在 block 内的编号，范围 [0, blockDim.x-1]

关键性质：不同 block 的执行顺序不确定。block 之间相互独立，调度由 GPU 决定。

2.4 二维/三维网格与线程块

gridDim 与 blockDim 类型为 dim3，有 x/y/z 三个成员；内建索引变量范围为：

blockIdx.{x,y,z} ∈ [0, gridDim.{x,y,z}-1]
threadIdx.{x,y,z} ∈ [0, blockDim.{x,y,z}-1]

二维/三维场景常用“复合索引”（全局坐标）：

nx = blockDim.x * blockIdx.x + threadIdx.x
ny = blockDim.y * blockIdx.y + threadIdx.y
nz = blockDim.z * blockIdx.z + threadIdx.z

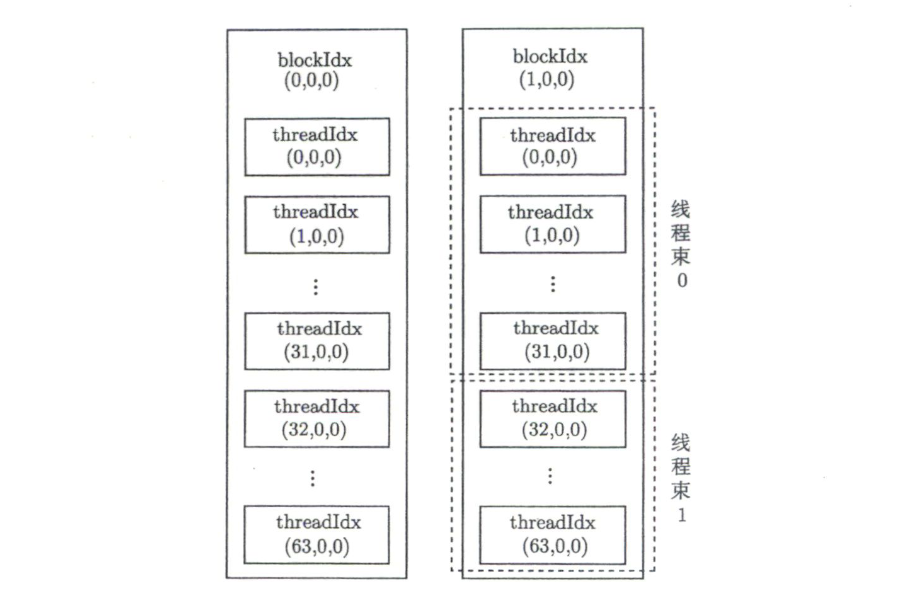
2.5 线程束（Warp）

warp 是 GPU 执行调度的基本单位：32 个线程为一组。
block 内线程按顺序每 32 个组成一个 warp。
多维 threadIdx 中，x 维度变化最快。

2.6 grid 与 block 尺寸的硬性上限

网格大小（gridDim）最大值：
- gridDim.x ≤ 2^31 − 1
- gridDim.y ≤ 65535
- gridDim.z ≤ 65535
线程块维度（blockDim）最大值：
- blockDim.x ≤ 1024
- blockDim.y ≤ 1024
- blockDim.z ≤ 64
线程块总线程数上限：
- blockDim.x * blockDim.y * blockDim.z ≤ 1024

2.7 CUDA 头文件包含规则（nvcc 编译时）

使用 nvcc 编译 .cu 时，会自动包含必要的 CUDA 头文件（如 <cuda.h>、<cuda_runtime.h>）。另外 <cuda.h> 会包含 <stdlib.h>，因此不少情况下无需显式包含 <stdlib.h>。若使用 CUDA 加速库，则需包含相应头文件并指定链接选项。

2.8 nvcc 编译流程与关键选项（虚拟架构 vs 真实架构）

nvcc 的核心流程：

将源码拆分为主机端（CPU）与设备端（GPU）代码。
设备端先编译成 PTX（虚拟架构中间代码），再编译成面向具体 GPU 的 cubin（机器码目标代码）。

关键选项：

-arch=compute_XY：指定虚拟架构（决定 PTX 可使用哪些 CUDA 特性）。
-code=sm_ZW：指定真实架构（决定最终生成给哪类 GPU 的机器码）。

约束关系：

真实架构必须 ≥ 虚拟架构
- 可以：-arch=compute_35 -code=sm_60
- 不可以反过来（会报错）

简化形式：

-arch=sm_XY 等价于：生成 sm_XY 的 cubin，并保留 compute_XY 的 PTX。

JIT（即时编译）与保留 PTX：

可用 -gencode arch=compute_XY,code=compute_XY 将 PTX 打包进可执行文件。
当遇到未预先生成 cubin 的新 GPU 时，驱动可在运行时对 PTX 进行 JIT，生成适配当前 GPU 的机器码。

未写选项时：

nvcc 会采用默认目标计算能力。

3. 简单的CUDA程序的基本框架

3.1 设备内存的动态分配与释放（cudaMalloc / cudaFree）

CUDA Runtime API 的函数通常以 cuda 开头：

cudaMalloc()：在设备内存（显存/线性内存）分配空间
cudaFree()：释放 cudaMalloc 分配的设备内存
cudaDeviceSynchronize()：同步 CPU 与 GPU

cudaMalloc 原型：

1	cudaError_t cudaMalloc(void **address, size_t size);

参数含义：

address：待被赋值的指针变量的地址（因此是二级指针）
size：分配字节数
返回值：错误码（成功为 cudaSuccess）

典型写法：

cudaMalloc((void**)&d_x, M);（常见：把 T** 强转 void**）
也可能写成 cudaMalloc(&d_x, M);（依赖隐式转换/编译器接受）

为什么传 void** / 二级指针？

cudaMalloc 需要修改指针本身（让 d_x 指向新分配的显存地址），因此必须传入 &d_x。
同时函数返回值用于返回错误码，不直接返回指针。

释放：

cudaFree(void* address)：参数是指针本身（非二级指针），返回值同样是错误码。

分配与释放必须配对：cudaMalloc ↔ cudaFree；malloc ↔ free；new ↔ delete，否则容易出错甚至段错误。

3.2 主机与设备之间的数据拷贝（cudaMemcpy）

在 cudaMalloc 分配好设备内存后，用 cudaMemcpy 在主机与设备之间传数据（计算前 H→D，计算后 D→H）。

原型：

1	cudaError_t cudaMemcpy(void* dst, const void* src, size_t count, enum cudaMemcpyKind kind);

参数含义：

dst：目标地址
src：源地址
count：拷贝字节数
kind：拷贝方向/类型

kind 常用取值：

cudaMemcpyHostToHost
cudaMemcpyHostToDevice
cudaMemcpyDeviceToHost
cudaMemcpyDeviceToDevice
cudaMemcpyDefault：根据指针地址自动判断方向（依赖 UVA，通常要求 64 位主机）

注意：

kind 必须与 src/dst 实际位置匹配，写错会报错。
Host→Device 选 cudaMemcpyHostToDevice（或 cudaMemcpyDefault）
Device→Host 选 cudaMemcpyDeviceToHost（或 cudaMemcpyDefault）

3.3 核函数中数据与线程的对应关系

主机端常用 for 循环逐元素处理；GPU 核函数采用 SIMT 思路：让每个线程负责一个（或少量）元素。

线程映射到数组下标：

n = blockDim.x * blockIdx.x + threadIdx.x

3.4 边界判断：为什么核函数里常常必须写 if

当 N 不是 block_size 的整数倍时，为覆盖所有元素通常会将 grid_size 向上取整，这会产生多余线程。若不做边界判断，多余线程会访问 x[n] / y[n] / z[n] 的越界位置，引发非法显存访问与不可预期错误。

典型写法：

计算全局索引 n
若 n >= N，直接返回

3.5 设备函数（device function）与函数执行空间限定符

设备函数：在 GPU 上执行、只能在 GPU 端被调用。核函数：也在 GPU 上执行，但通常由 CPU 端通过 <<<>>> 启动（动态并行时也可由设备端发起）。

执行空间标识符：

__ global__：核函数（一般主机端调用、设备端执行；动态并行时设备端也可发起）。
__ device__：设备函数（只能设备端调用，在设备端执行）。
__ host__：主机函数（主机端调用/执行；普通 C++ 函数通常可省略）。
可写 __ host__ __ device__：同一函数同时生成 CPU 版与 GPU 版，减少重复代码（编译器分别编译）。
不能同时使用：

__ device__ 与 __ global__
__ host__ 与 __ global__

内联控制：

编译器自行决定是否内联；
可用 __ noinline__ 建议不内联，__ forceinline__ 建议强制内联（不保证一定生效）。

4. CUDA程序的错误检测

4.1 运行时错误的基本定位思路

CUDA 错误大致分为：

编译错误：编译阶段即可发现。
运行时错误：编译不报错，但运行时出错，更难排查。

检查 Runtime API 返回值：

多数 Runtime API（如 cudaMalloc / cudaMemcpy / cudaFree）返回 cudaError_t。
返回 cudaSuccess 才表示成功。

建议封装检查宏 CHECK(call)（如放到 error.cuh），宏内部流程：

保存返回值 cudaError_t error_code
判断是否为 cudaSuccess
若失败：打印文件名、行号、错误码、错误字符串并退出
cudaGetErrorString() 用于把错误码转为可读信息

多数 Runtime API 推荐都用 CHECK 包住；但例如 cudaEventQuery() 可能返回 cudaErrorNotReady，不一定表示程序出错。

4.2 核函数调用错误的检查

核函数本身不返回错误码。典型调试写法是在每次 kernel launch 后加：

CHECK(cudaGetLastError());：获取最近一次 CUDA 错误（通常是 launch 配置/参数等错误）
CHECK(cudaDeviceSynchronize());：由于 kernel launch 异步，必须同步才能把执行期间错误“逼出来”

注意：

cudaDeviceSynchronize() 很耗时，尤其在内层循环中会严重影响性能；一般仅用于调试或必要同步。
后续若调用可能隐式同步的 API（如 cudaMemcpy），也可能捕获到前面 kernel 的错误，但为了定位精确，调试时更推荐显式同步。

调试技巧：将 kernel 调用临时变成同步

设置环境变量 CUDA_LAUNCH_BLOCKING=1（一般仅用于调试，影响性能）

4.3 用CUDA-MEMCHECK工具集检查CUDA程序的内存错误

CUDA-MEMCHECK 是一套内存/并发错误检测工具，包含四个子工具：

memcheck：内存访问错误（越界、非法地址等）
racecheck：竞争条件（常见于共享内存等）
initcheck：未初始化内存使用
synccheck：同步相关问题

统一入口：

1	cuda-memcheck --tool <toolname> [options] app_name [options]

其中 memcheck 可简写为：

1	cuda-memcheck [options] app_name [options]

5. 获得GPU加速的关键

5.1 用 CUDA Event 计时（面向CUDA代码的计时方式）

CUDA event 计时流程可概括为：

record(start) → 执行 → record(stop) → 同步 → elapsed → destroy

典型步骤：

定义 cudaEvent_t start, stop
cudaEventCreate() 创建事件
cudaEventRecord(start, stream) 记录开始
执行待计时代码（主机代码 / kernel / 混合）
cudaEventRecord(stop, stream) 记录结束
cudaEventSynchronize(stop) 等待 stop 完成
cudaEventElapsedTime(&ms, start, stop) 计算耗时（毫秒）
cudaEventDestroy() 销毁事件

5.2 用条件编译控制单/双精度（示例）

定义 USE_DP 时：real = double，EPSILON = 1e-15
否则：real = float，EPSILON = 1e-6

编译示例：

单精度：nvcc -O3 -arch=sm_75 xxx.cu
双精度：nvcc -O3 -arch=sm_75 -DUSE_DP xxx.cu

观察：数组相加核函数单精度（约 3.3ms）与双精度（约 6.8ms）时间比值约 2。
但“约 2 倍”不等价于 GPU 单/双精度峰值算力比，因为数组相加更可能是带宽受限。

5.3 计算有效显存带宽（以数组相加为例）

数组相加：z[i] = x[i] + y[i]，长度。以 float 为例：

每元素4B，
每元素访问流量：读 x[i] 4B + 读 y[i] 4B + 写 z[i] 4B ⇒ 共约 12B/元素

总数据量：

若核函数时间，则带宽：

理论显存带宽 448GB/s，而测得约 360GB/s，说明该 kernel 属于典型 memory-bound：算术运算占比可忽略。

5.4 Host↔Device 拷贝时间可能压倒一切

将 Host↔Device 拷贝时间也计入后，总耗时被拷贝主导：

单精度：拷贝 + 核函数总计约 180ms
双精度：约 360ms
核函数本身只占极小比例（文中提到不到拷贝时间的 2% 量级）

结论：若任务仅是 “CPU传两数组 → GPU相加 → 传回CPU”，GPU 可能不但不加速，反而更慢。

5.5 用 nvprof / nsys 定位瓶颈

nvprof 示例：

nvprof ./a.out
若出现 Unified Memory profiling 报错：
nvprof –unified-memory-profiling off ./a.out

说明：本机环境为 CUDA 13.x（/usr/local/cuda-13、cuda-13.1），CUDA 12 及以后 nvprof 已被移除，可用 Nsight Systems（nsys）：

nsys profile --trace=cuda -o report ./a.out
nsys stats report.nsys-rep --report cuda_gpu_mem_time_sum
nsys stats report.nsys-rep --report cuda_gpu_kern_sum
nsys stats report.nsys-rep --report cuda_api_trace,cuda_gpu_trace

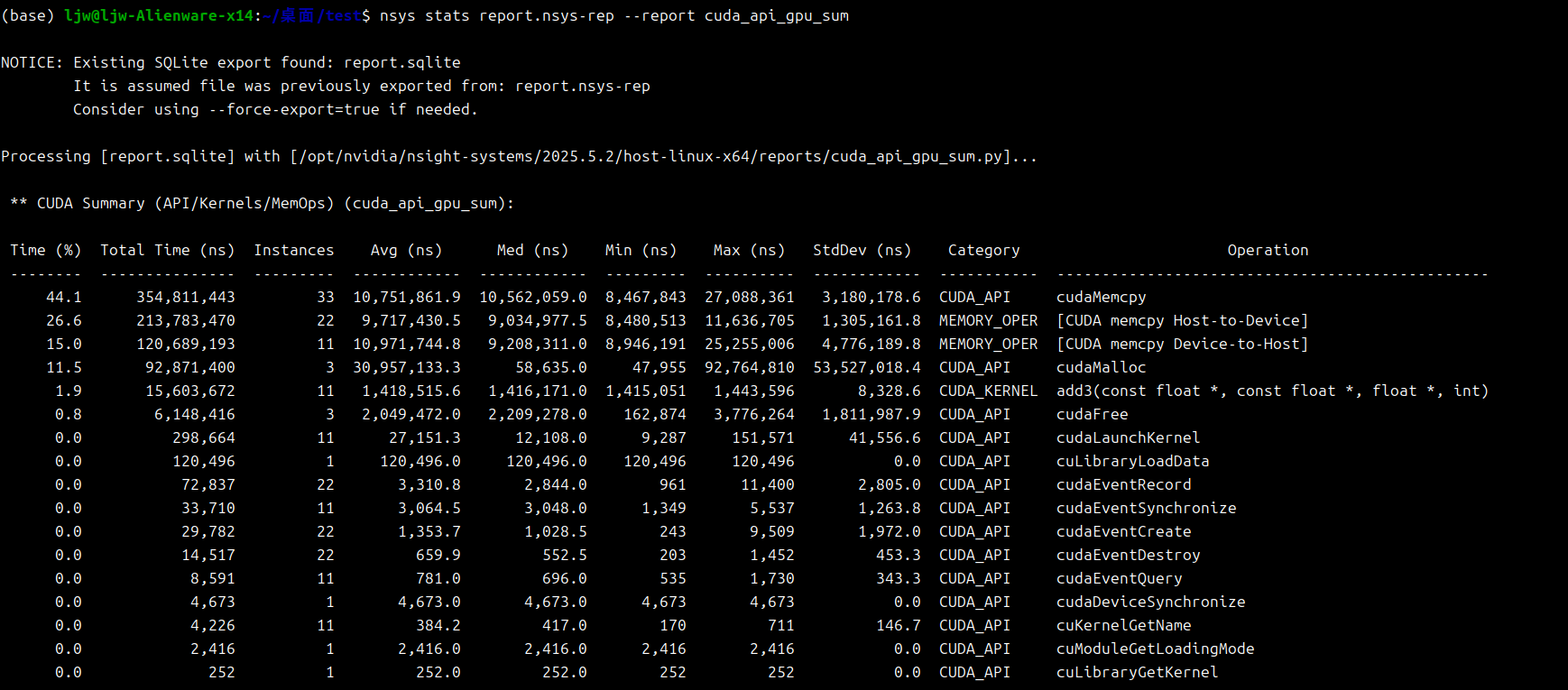
典型观察：主要时间在

[CUDA memcpy HtoD]
[CUDA memcpy DtoH]
kernel add() 只占极小比例

进一步结论：很多时候瓶颈不在算，而在数据搬运。

5.6 影响GPU加速的三大关键因素

数据传输的比例
算术强度
并行规模

5.6.1 数据传输比例

GPU 内部显存带宽高（数百 GB/s），但 CPU 内存 ↔ GPU 显存通常通过 PCIe 等总线，带宽低得多（例如 PCIe x16 Gen3 约 16GB/s），差一个数量级以上。

因此要获得明显加速，关键是：

减少 CPU↔GPU 往返次数与占比
尽量把可连续执行的计算都留在 GPU 上
典型策略：把“只算一次”改成“在 GPU 上重复算很多次”，只在开始/结束各传一次数据

5.6.2 算术强度（AI）与FMA

算术强度（AI）定义：单位数据传输（按字节）对应的浮点运算次数（按 FLOPs）。

AI 低：搬数据多、计算少 ⇒ 常为 memory-bound
AI 高：搬一次数据算很多次 ⇒ 更可能 compute-bound

提高 AI 的直觉方式：

在寄存器/共享内存里复用数据，多算几次少搬几次
引入更多 FLOPs 而不显著增加访存

FMA（Fused Multiply-Add）：

指令形式：d=a×b+c
融合乘加通常只做一次舍入，精度与速度都更好
性能统计中常按 2 FLOPs 计（一次乘法 + 一次加法）

5.6.3 理论寄存器带宽（量级启发）

把峰值 FLOPS 换算成“数据供给速度”的量级直觉：若计算单元持续满速做 FMA，寄存器级数据周转需要达到 TB/s 量级。

以 RTX 2070 单精度峰值约。为例：

单精度每数 4B
a,b,c,d 共涉及约 4×4B
一个 FMA 按 2 FLOPs 计

所以理论寄存器带宽：

这说明：显存只有几百 GB/s，若任务频繁从显存取数且计算不足，就容易撞上带宽墙。（该推导用于量级比较，不等同于可直接测得的真实寄存器物理带宽。）

5.7 加速比与算术强度的关系（示例总结）

数组相加核函数在 RTX 2070 上相对未深度优化的 CPU 版本可快约 20×，但很难继续提升，因为 AI 太低（读两次写一次只算一次加法）。

提高 AI 的方法：让每次读写对应更多计算，例如对每元素做 10000 次循环并加入 sqrt 等复杂运算。

据示例：

当数组长度：
- CPU 时间约 320ms（单精度）/ 450ms（双精度）
当数组长度：
- GPU 核函数时间约 28ms（单精度）/ 1000ms（双精度）
根据处理规模差（100×）估算加速比：
- 单精度：
- 双精度：

5.8 单精度 vs 双精度：GeForce 与 Tesla 的差异（高AI场景）

当计算主导（AI 高）时：

GeForce 单精度性价比高
双精度能力通常显著弱于 Tesla

例子：

RTX 2080 Ti：单精度 15ms，双精度 450ms，差约 30×
Tesla V100：单精度 11ms，双精度 28ms，只差约 2×

低 AI 场景（如数组相加）下，Tesla 相对 GeForce 的优势不一定明显。

5.9 并行规模（Parallelism Scale）与“吃饱GPU”

并行规模可近似理解为 kernel 启动的总线程数。GPU 由多个 SM 组成，每个 SM 可同时驻留线程数有上限（笔记给出：一般可到 2048，某些如图灵约 1024）。若启动线程总数远小于可驻留线程规模，会导致大量资源空闲，加速比不明显。

实验现象（将 𝑁 从逐步增到：

𝑁 大：GPU 满负荷，kernel 时间近似正比于 𝑁
𝑁 小：kernel 时间接近常数“底噪”（启动/调度/固定开销 + 资源未充分利用）

加速比随 𝑁 增大先快速上升后趋于饱和：

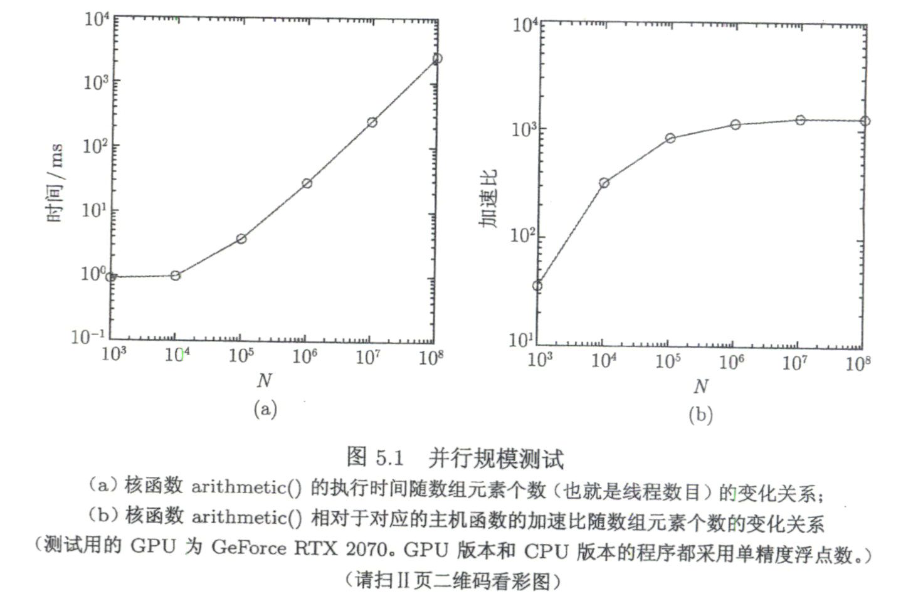
结论：除了算术强度，还要确保线程规模足够大以充分利用 SM，否则很难获得可观加速。

5.10 CUDA 数学函数库：math functions vs intrinsics

CUDA Math API 提供大量数学函数（开方、三角、指数对数等）。函数分层概念：

数学函数（math functions）：通常精度更有保证、实现更通用
内建函数（intrinsics）：通常更快但可能精度/约束更严格，更贴近硬件行为

以平方根为例：

double sqrt(double x);
float sqrt(float x);
float sqrtf(float x);

内建版本（不同舍入模式），例如：

float：__fsqrt_rd / __fsqrt_rn / __fsqrt_ru / __fsqrt_rz
double：__dsqrt_rd / __dsqrt_rn / __dsqrt_ru / __dsqrt_rz

实践中需结合数值精度要求选择：单/双精度、普通函数/内建函数。

6. CUDA的内存组织

6.1 分层内存（Memory Hierarchy）

CPU/GPU 都采用分层内存结构，不同层级在容量、延迟、可见性、生命周期等方面差异显著。一般规律：

越快（延迟低）容量越小
越慢（延迟高）容量越大

典型策略：热数据尽量放在更快层级，冷数据放在更大更慢层级。分层能降低平均访存延迟、提高效率。

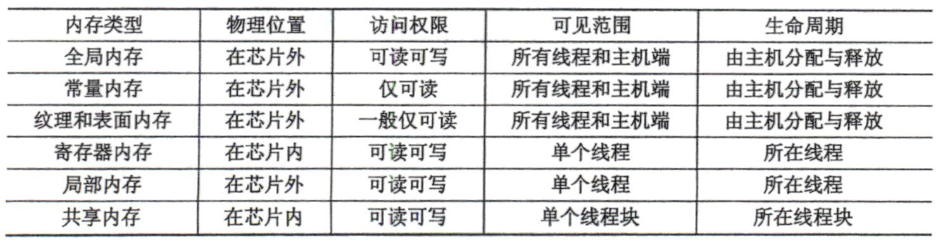
按物理位置/访问权限/可见范围/生命周期等维度，常见内存类型包括：

全局内存（Global）：芯片外；可读写；对所有线程及主机可见；主机端分配/释放。
常量内存（Constant）：芯片外；只读；对所有线程及主机可见；主机端分配/释放。
纹理/表面内存（Texture/Surface）：芯片外；纹理通常只读；表面更灵活（可写）；对所有线程及主机可见；主机端分配/释放。
寄存器（Register）：芯片内；可读写；线程私有；生命周期=线程。
局部内存（Local）：物理上通常在芯片外（寄存器溢出/编译器安排）；线程私有；生命周期=线程。
共享内存（Shared）：芯片内；可读写；块内共享（block 范围）；生命周期=线程块。

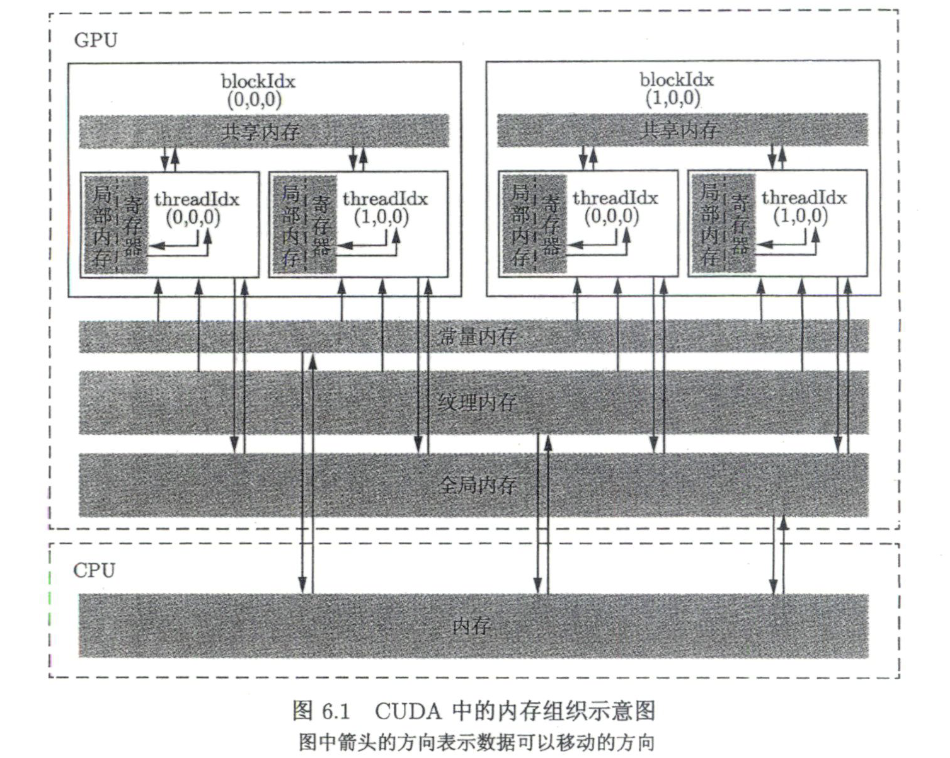
图示强调的数据访问关系（以 block/thread 层级为线索）：

线程访问寄存器/局部内存
block 内线程可通过共享内存协作
grid 内不同 block 可通过全局内存交换数据
常量/纹理提供缓存友好只读路径
主机与设备之间通过数据传输建立数据流动

6.2 全局内存（Global Memory）

全局内存（global memory）是核函数中所有线程都能访问的设备内存。特点：

不在芯片上 ⇒ 延迟高、访问慢
容量最大（基本等同显存容量）
承担主机↔设备传输、设备↔设备拷贝等

动态分配与释放：

cudaMalloc() 分配
cudaMemcpy() 传输
cudaFree() 释放

拷贝方向：

Host → Device：cudaMemcpyHostToDevice
Device → Host：cudaMemcpyDeviceToHost
Device → Device：cudaMemcpyDeviceToDevice（或 cudaMemcpyDefault 视情形）

全局内存生命周期由主机端控制：从 cudaMalloc 开始到 cudaFree 结束，在此期间可被多个核函数多次访问。

全局内存属于线性内存（linear memory）。二维/三维数据可用：

cudaMallocPitch() / cudaMalloc3D() 分配
cudaMemcpy2D() / cudaMemcpy3D() 拷贝
以及 CUDA Array（对用户不透明，主要服务纹理访问）

静态全局内存变量（编译期确定大小）：

1 2	__device__ T x; __device__ T y[N];

设备端可直接访问这些 __ device__ 变量；主机端不能直接读写，但可用：

cudaMemcpyToSymbol()：Host → Device symbol
cudaMemcpyFromSymbol()：Device symbol → Host

原型：

cudaError_t cudaMemcpyToSymbol(
  const void* symbol,      // 静态全局内存变量名
  const void* src,         // 主机内存缓冲区指针
  size_t      count,       // 复制的字节数
  size_t      offset = 0,  // 从 symbol 对应设备地址开始偏移的字节数
  cudaMemcpyKind kind = cudaMemcpyHostToDevice  // 可选参数
);

cudaError_t cudaMemcpyFromSymbol(
  void*       dst,         // 主机内存缓冲区指针
  const void* symbol,      // 静态全局内存变量名
  size_t      count,       // 复制的字节数
  size_t      offset = 0,  // 从 symbol 对应设备地址开始偏移的字节数
  cudaMemcpyKind kind = cudaMemcpyDeviceToHost  // 可选参数
);

总结：全局内存是容量最大但最慢的设备内存，承担主要数据存储与主机/设备数据传输；可动态管理，也可通过 device 静态符号结合 cudaMemcpyTo/FromSymbol 与主机交换数据。

6.3 常量内存（Constant Memory）

常量内存是带常量缓存（constant cache）的全局只读区域：

容量很小（如 64KB）
对所有线程及主机可见
由主机端管理
设备端只读，不可写

性能要点：

当同一 warp 内线程读取相同地址时，可利用缓存/广播机制显著加速。

典型用法：

用 __ constant__ 定义常量变量
用 cudaMemcpyToSymbol() 把数据从主机拷入常量内存
kernel 内直接读取该常量变量

额外说明：

当计算能力 ≥ 2.0 时，核函数“按值传递”的参数会放在常量内存里。
通过参数使用常量内存有上限：每个核函数最多约 4KB 常量内存用于存放这些参数（可包含结构体与固定数组等）。

总结：常量内存=小容量（64KB）只读全局区，带缓存；warp 内同地址读取效率很高；使用 __ constant__ + cudaMemcpyToSymbol 管理；按值参数本质上也会占用一小段常量内存（≤约 4KB/核函数）。

6.4 纹理/表面内存与只读缓存（__ldg）

纹理内存（texture memory）与表面内存（surface memory）类似常量内存：属于带缓存的全局内存区域，容量通常更大；访问方式通过绑定与专用接口，常用于图像/采样类访问模式。纹理通常只读；表面更灵活（可写）。

只读缓存路径：

计算能力 ≥ 3.5 的 GPU，可对只读全局数据使用 __ldg() 走只读数据缓存。
原型：T __ldg(const T* address);

说明：

Pascal 及更高架构，很多情况下编译器会默认利用类似只读缓存路径，因此不一定需要显式调用 __ldg()。

6.5 寄存器（Register）

在核函数中定义的、未加限定符的局部变量通常放在寄存器中。数组可能被放进寄存器，但也可能因为寄存器不足或编译器策略而落到局部内存。gridDim/blockDim/blockIdx/threadIdx/warpSize 等内建变量在特殊寄存器中，访问高效。

特性：

线程私有：每个线程一份副本
生命周期：随线程开始到结束
速度最快但数量有限，影响性能调优（如占有率、可驻留线程数）
寄存器以 32-bit 为单位，一个 double（64-bit）通常占用两个寄存器

6.6 局部内存（Local Memory）

局部内存从编程模型上看类似线程私有变量，但硬件上通常落在全局内存（芯片外），因此慢。常见触发原因：

寄存器溢出（register spill）
编译器无法把对象放进寄存器（例如索引在编译期不可确定的数组）
由编译器决定是否使用局部内存

特点：

线程私有
生命周期=线程
物理上在全局内存 ⇒ 延迟高
每线程局部内存可达 512KB，但越多通常越慢，应尽量避免过多使用

6.7 共享内存（Shared Memory）

共享内存位于芯片上（on-chip），速度仅次于寄存器，远快于全局/局部内存；但容量有限，是稀缺资源。

关键差异（相对寄存器）：

可见范围：线程块（block）内共享
每个 block 有自己的一份共享内存副本；不同 block 互不可见
生命周期：随线程块开始到结束

主要价值：

减少全局内存访问次数（数据复用）
改善全局内存访问模式（例如分块、重排、提高合并度）

资源约束：

共享内存上限随架构变化（48KB/64KB/96KB 等常见量级）
与寄存器一起会影响能同时驻留的 block 数量与最终性能

6.8 L1 / L2 缓存（概念与架构差异）

从 Fermi 开始，GPU 提供：

SM 级 L1 缓存
设备级 L2 缓存（多个 SM 共享）

主要用于缓存全局内存与局部内存访问，降低延迟。架构差异（按笔记保留）：

Kepler：L1 与共享内存共享物理资源
Maxwell/Pascal：L1 与纹理缓存合并，共享内存独立
Volta/Turing：L1/纹理/共享内存三者统一为统一资源

共享内存是“可编程缓存”，L1/L2 是“不可编程缓存”。

容量配比：

CC 3.5：L1+共享合计 64KB，共享可设 16/32/48KB，默认 48KB
CC 3.7：合计 128KB，共享可设 80/96/112KB，默认 112KB
Maxwell/Pascal：不允许调整共享上限
Volta：统一缓存合计 128KB，共享可设 0/8/16/32/64/96KB
Turing：统一缓存合计 96KB，共享可设 32KB 或 64KB

6.9 SM 与占有率（Occupancy）

SM（Streaming Multiprocessor）包含寄存器、共享内存、各类缓存、warp 调度器、执行单元（INT32/FP32/FP64/SFU/Tensor Cores 等）。

占有率（occupancy）：SM 上实际驻留线程数/线程块数相对硬件上限的比例。

100% 占有率不是高性能的充分/必要条件
但占有率过低（例如 <25%）通常容易性能差
并行规模太小会导致部分 SM 根本没被使用（占有率为 0）

在并行规模足够大前提下，占有率受两类硬上限约束：

单个SM最多可同时驻留的线程块数：（开普勒、图灵）或（麦克斯韦、帕斯卡、伏特等）
单个 SM 最多可同时驻留的线程数：（开普勒到伏特）或（图灵）

6.10 限制占有率的三类关键因素

线程块大小（block size）

warp 为 32 线程，block size 最好为 32 的整数倍，否则会浪费。
在 block size 为 32 整数倍的前提下：若 block size 不小于且能整除，才可能达到 100% 占有率。
- 开普勒：block size ≥ 128 时可达 100%
- 其他一些架构：block size ≥ 64 时可达 100%

寄存器数量限制。

某些计算能力下每 SM 可用寄存器总量为 64K（64×1024 个 32-bit 寄存器）。
若，，则平均每线程最多约：
即要满线程时每线程寄存器数最好不超过约 32。若核函数每线程寄存器数 > 32，占有率会下降。
- 每线程寄存器数 > 64 ⇒ 占有率可能 < 50%
- 每线程寄存器数 > 128 ⇒ 占有率可能 < 25%

共享内存数量限制。

以 CC 3.5 为例：若 block size=128，要满 2048 线程需 16 个 block。
- 100% 占有率：每 block ≤ 约 3KB 共享内存
- 50% 占有率：每 block ≤ 约 6KB
- 25% 占有率：每 block ≤ 约 12KB
- 若每 block > 48KB，kernel 可能无法运行

工具/编译信息：

CUDA_Occupancy_Calculator.xls 可估算占有率
–ptxas-options=-v 可报告每个 kernel 的寄存器使用数
可用 __ launch_bounds__() 与 –maxrregcount 控制寄存器使用

6.11 查询设备信息：cudaDeviceProp

核心结构体：cudaDeviceProp，常用 API：

cudaGetDeviceProperties()：查询某 device_id 的属性
cudaSetDevice()：选择要使用的 GPU（多卡常见）

示例代码：

#include "error.cuh"
#include <stdio.h>

int main(int argc, char *argv[])
{
    int device_id = 0;
    if (argc > 1) device_id = atoi(argv[1]);
    CHECK(cudaSetDevice(device_id));

    cudaDeviceProp prop;
    CHECK(cudaGetDeviceProperties(&prop, device_id));

    printf("Device id:                                 %d\n",
        device_id);
    printf("Device name:                               %s\n",
        prop.name);
    printf("Compute capability:                        %d.%d\n",
        prop.major, prop.minor);
    printf("Amount of global memory:                   %g GB\n",
        prop.totalGlobalMem / (1024.0 * 1024 * 1024));
    printf("Amount of constant memory:                 %g KB\n",
        prop.totalConstMem  / 1024.0);
    printf("Maximum grid size:                         %d %d %d\n",
        prop.maxGridSize[0], 
        prop.maxGridSize[1], prop.maxGridSize[2]);
    printf("Maximum block size:                        %d %d %d\n",
        prop.maxThreadsDim[0], prop.maxThreadsDim[1], 
        prop.maxThreadsDim[2]);
    printf("Number of SMs:                             %d\n",
        prop.multiProcessorCount);
    printf("Maximum amount of shared memory per block: %g KB\n",
        prop.sharedMemPerBlock / 1024.0);
    printf("Maximum amount of shared memory per SM:    %g KB\n",
        prop.sharedMemPerMultiprocessor / 1024.0);
    printf("Maximum number of registers per block:     %d K\n",
        prop.regsPerBlock / 1024);
    printf("Maximum number of registers per SM:        %d K\n",
        prop.regsPerMultiprocessor / 1024);
    printf("Maximum number of threads per block:       %d\n",
        prop.maxThreadsPerBlock);
    printf("Maximum number of threads per SM:          %d\n",
        prop.maxThreadsPerMultiProcessor);

    return 0;
}

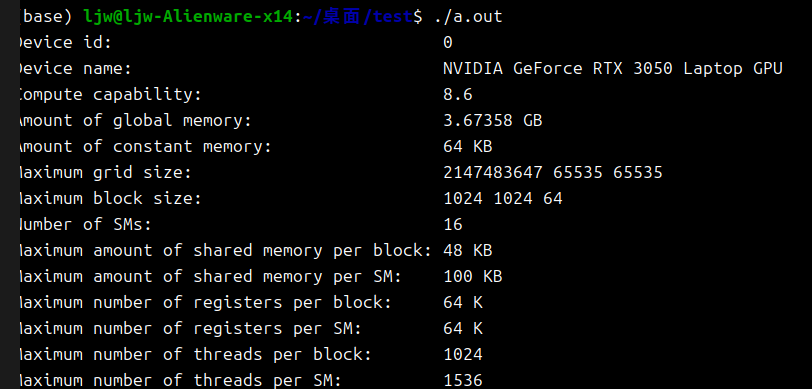
结论：cudaDeviceProp + cudaGetDeviceProperties() 是编写通用、高性能 CUDA 代码的重要基础步骤，用于让程序“认识自己运行在哪张 GPU 上”。

7. 全局内存的合理使用

7.1 全局内存访问与内存事务

全局内存访问本质上会触发内存事务（memory transaction）：线程对全局内存的读写，会在缓存（L1/L2）与DRAM之间产生数据搬运。

当有 L1/L2 缓存时：读取全局内存通常先查 L1，再查 L2，若仍不命中才访问 DRAM。为便于讨论，本节以“主要考虑 L2 缓存”的简化模型为例：一次数据传输默认搬运 32 字节（一个 cache sector）。

7.2 合并访问（coalesced）与非合并访问（uncoalesced）

合并访问（coalesced）：一个 warp（32线程）发起的一次读/写请求，能够用尽可能少的 32B 事务完成。
非合并访问（uncoalesced）：同样的访问需求需要更多次 32B 事务才能满足，导致带宽浪费。

定义合并度（degree of coalescing）：
$合并度实际需要的字节数为该请求触发的数据传输总字节数$ 。

如果每次传输搬来的数据都被用上 → 合并度100%。

7.3 32线程读取 float 的理想合并情形

warp 内 32 个线程，每线程读 1 个 float（4B），warp 实际需要：
如果地址对齐且连续，128B可以由4次32B传输完成：
$合并度$ 。

对齐要求：32B 事务的首地址必须是 32B 的整数倍（典型覆盖区间：0–31、32–63、…）。另外，cudaMalloc 分配的起始地址通常至少 256B 对齐，有利于合并访问。

7.4 五种典型访问模式与合并度对比

顺序的合并访问（add）
- 全局索引：n = blockIdx.x * blockDim.x + threadIdx.x
- warp 访问连续的 x[0..31] 等 → 4次事务 → 合并度 100%
乱序/交叉的合并访问（add_permuted）
- 例如用 threadIdx.x ^ 0x1 交换相邻线程的访问顺序
- 虽然“线程号 ↔ 元素号”不再一一对应，但 warp 访问的地址集合仍落在同一段连续区间 → 仍是 4次事务 → 合并度 100%
  
  合并关注的是 warp 访问地址的分布，而不要求线程按顺序访问。
不对齐的非合并访问（add_offset）
- 让 warp 访问 x[1..32]，跨越了 32B 分段边界
- 覆盖 128B 需要 5次事务 → 合并度：
跨越式（stride）非合并访问（add_stride）
- n = blockIdx.x + threadIdx.x * gridDim.x
- 同一 warp 访问元素彼此间隔很大（如 0,128,256,384…）
- 这些地址分散在大量不同的 32B 片段中，可能触发 32次事务才凑够 128B → 合并度：
广播式非合并访问（add_broadcast）
- warp 内所有线程都读同一个 x[0]。
- 只需 1次 32B 事务即可取到 x[0]，但 warp 实际只用到其中 4B → 合并度：
  
  这种“所有线程读同一地址”的模式更适合放到常量内存，利用常量缓存/广播机制。

7.5 合并访问的本质总结

合并访问的目标是：让一个 warp 的访问尽量落在尽量少的、对齐的 32B 段里，从而用最少事务搬到“刚好够用”的数据。

不对齐、跨步、广播等模式都会降低合并度，造成带宽浪费并拖慢性能。

7.6 矩阵复制：作为转置优化的基准

在讨论转置前，先建立一个更简单的基准：矩阵复制（copy），并用它说明 2D grid/block 划分与合并访问的关系。

7.6.1 tile 思想与 TILE_DIM=32

将大矩阵切成多个 32×32 小块（tile）
TILE_DIM 是整数常量，可写：
- const int TILE_DIM = 32; 或 #define TILE_DIM 32
在核函数中可直接使用该常量值，但避免对其取地址/引用

7.6.2 2D 网格与 2D 线程块配置

blockDim = (32, 32)，每个 block 有 32×32=1024 线程（常见上限）
若矩阵边长为 N 且可被 32 整除，则：
- gridDim = (N/32, N/32)
- 例如 N=128：gridDim.x=gridDim.y=4，即 4×4 blocks

7.6.3 copy 的索引与合并访问原因

用 (threadIdx.x, threadIdx.y) 表示 tile 内列/行坐标
结合 (blockIdx.x, blockIdx.y) 得到全局坐标 (nx, ny)
线性下标：idx = ny * N + nx
threadIdx.x 是变化最快的维度，因此相邻线程通常对应相邻列（也即一维下标相邻）
→ 读 A 与写 B 都呈连续地址访问
→ 属于顺序合并访问

7.6.4 带宽测量（RTX 2080Ti，N=10000，单精度）

copy 核函数时间约 1.6 ms
有效带宽：
- 元素数：
- 每元素 float：4B
- copy 每元素流量：读 4B + 写 4B = 8B
- 总字节数：
- 用时：
- 带宽：
结果：约 500 GB/s，小于理论 616 GB/s（符合“实际 < 理论”的常见现象）

7.7 仅用全局内存实现矩阵转置：读写必有一个不合并

矩阵复制：
转置可写成两种等价实现（对应两种核函数）：

transpose1：
transpose2：

两者都正确，但访问模式不同：

7.7.1 不考虑对齐细节时的访问模式对比

transpose1：
- 读 A：合并（按行读）
- 写 B：非合并（跨行写，写很分散）
transpose2：
- 读 A：非合并（按列读，stride大）
- 写 B：合并（按行写）

因此它们都是“一个合并 + 一个非合并”，区别在于非合并发生在读还是写。

7.7.2 性能结论（RTX 2080Ti，单精度）

transpose1：约 5.3 ms
transpose2：约 2.8 ms（更快）

原因倾向：在 transpose2 中，虽然读 A 非合并，但只读缓存路径可能缓解读的代价：从 Pascal 起，编译器若判断数据只读，会倾向用 __ldg() 或等效机制走只读缓存；而全局写入没有类似的“写缓存捷径”，因此非合并写通常更难优化，成为 transpose1 的主要瓶颈。

结论倾向：当读写无法同时合并时，通常更优先保证写合并。

7.7.3 老架构的相反现象（K40：Kepler）

Kepler / Maxwell 默认不会自动走 __ldg()
K40（单精度）测试：
- transpose1：约 12 ms（更快）
- transpose2：约 23 ms（更慢）
解决：在这些架构上显式使用 __ldg() 形成 transpose3：
1
B[nyN+nx]=\_\_ldg(&A[nxN+ny])
K40 上 transpose3 约 8 ms，优于 transpose1。

除了用只读缓存缓解“非合并读”，更强的办法是：用共享内存把非合并的全局访问“重排”为合并访问。

8. 共享内存的合理使用

8.1 共享内存的核心作用

共享内存是程序员可控的片上缓存，主要用途有两类：

减少全局内存访问次数，并支持线程块内的高效通信/协作
提高全局内存访问的合并度（通过“中转/重排”使全局读写更连续）

8.2 数组归约（reduction）：为什么需要同步

目标：给定长度为 𝑁 的数组 x，计算总和 sum。示例：N = 10^8，元素初始化为 1.23，计时 reduce()。

8.2.1 CPU 精度现象

双精度：前 9 位有效数字大体正确，后面逐渐有误差
单精度：可能出现“完全不对”，原因是累加时出现“大数吃小数”（float 只有约 6–7 位有效数字，累加到几千万后再加 1.23 可能被舍入掉）

CPU 版大约 100 ms（单/双精度差不多）。
（更稳健的求和可用 Kahan 等算法，但此处聚焦 CUDA 的并行实现与性能。）

8.2.2 “天真并行归约”为何不正确

归约不是逐元素独立计算，而是多轮折半迭代（binary reduction）。如果在一个 kernel 中直接写多轮：

若：d_x[n] += d_x[n+N/2]
若：d_x[n] += d_x[n+N/4]
…

8.2.3 解决：block 内同步 __syncthreads()

__syncthreads() 保证同一 block 内所有线程到达同步点后再继续，仅同步 block 内线程，不同步不同 block。

一个 block 归约的基本结构：

每个 block 处理 blockDim.x 个元素，例如：
- real *x = &d_x[blockDim.x * blockIdx.x];
典型要求（基础版本）：
- 𝑁 能被 blockDim.x 整除
- blockDim.x 是 2 的幂（如 128）
block 内 offset 折半：offset >>= 1，每轮之间 __syncthreads()

该步骤把长度的数组归约为长度的数组 d_y（每个 block 一个部分和）。若要最终总和，可先把 d_y 拷回主机再归约（但不够高效）。

性能（RTX 2070，单精度）：总耗时（kernel + 拷回 d_y + CPU收尾）约 5.8 ms，约为 CPU 的 17×（100/5.8）。

8.3 使用共享内存做数组归约：减少全局访存

前一版归约对全局内存读写频繁；全局内存慢，寄存器快但线程私有，不利于线程协作。归约需要 block 内线程协作，因此共享内存更合适。

8.3.1 基本做法

kernel 内定义共享内存：
- __ shared__ real s_y[128];
每个 block 有独立副本；block 内线程共享同一份 s_y

8.3.2 共享内存版流程

全局 → 共享：把 block 负责的数据拷到 s_y
- 可用 if (n < N) 做越界保护；越界线程写 0
__syncthreads()：保证共享数据就绪
共享内存内折半归约：在 s_y 上反复读写完成归约
if (tid==0)：把 s_y[0] 写回 d_y[bid]
共享内存生命周期只在 kernel 内，必须在结束前写回结果

8.3.3 性能观察

RTX 2070：用不用共享内存，总时间都差不多（约 5.8 ms）
Tesla K40（Kepler）：共享内存版更快（如 16.3 ms → 10.8 ms）

共享内存版相对只用全局内存的版本：

不再要求 𝑁 必须整除 block 大小（更通用）
归约过程中不修改原始全局数组 d_x（更安全、更符合实际）

8.4 动态共享内存：提升灵活性与可维护性

固定写死 __ shared__ real s_y[128]; 容易在修改 block_size 时忘记同步修改数组长度，导致越界或性能问题。

动态共享内存方案：

launch 配置中加入第三参数（动态共享字节数）：
- <<<grid, block, sizeof(real)*block>>>
kernel 内声明：
- extern __ shared__ real s_y[];
- 必须 extern，不能写长度；也不能写成 extern shared real *s_y;

性能上动态与静态共享内存通常接近；动态共享主要价值是：更不易写错、更灵活、更好维护。

8.5 共享内存实现矩阵转置：把非合并“重排”为合并

不用共享内存的转置里，读/写至少有一个会非合并。共享内存可作为中转区，使：

从 A 的读是合并的
向 B 的写也是合并的
转置动作在共享内存中完成，全局内存只承担顺序读/顺序写。

8.5.1 tile 转置基本流程

每个 block 处理一个 32×32 tile
kernel 内声明二维共享数组 S[32][32]

合并读：A → S（按行连续加载）
__syncthreads()
合并写：S → B（通过交换 threadIdx.x/threadIdx.y 的映射，使写回连续）

示例代码：

// bank.cu中利用共享内存进行矩阵转置但有bank冲突的核函数
__global__ void transpose1(const real *A, real *B, const int N)
{
    __shared__ real S[TILE_DIM][TILE_DIM];
    int bx = blockIdx.x * TILE_DIM;
    int by = blockIdx.y * TILE_DIM;

    int nx1 = bx + threadIdx.x;
    int ny1 = by + threadIdx.y;
    if (nx1 < N && ny1 < N)
    {
        S[threadIdx.y][threadIdx.x] = A[ny1 * N + nx1];
    }
    __syncthreads();

    int nx2 = bx + threadIdx.y;
    int ny2 = by + threadIdx.x;
    if (nx2 < N && ny2 < N)
    {
        B[nx2 * N + ny2] = S[threadIdx.x][threadIdx.y];
    }
}

8.5.2 性能对比（RTX 2080Ti，单精度）

共享内存转置：约 3.5 ms
比原 transpose1（全局内存写非合并）5.3 ms 更快
但仍慢于 transpose2（全局内存读非合并）2.8 ms

8.6 共享内存 bank 机制

为提供高带宽，共享内存被硬件划分为 32 个 bank（0–31），对应一个 warp 的 32 个线程。
在“非开普勒架构”中，bank 宽度通常是 4B（一个 32-bit word）。

对 float（32-bit）访问：

word_index = address / 4
bank_id = word_index mod 32

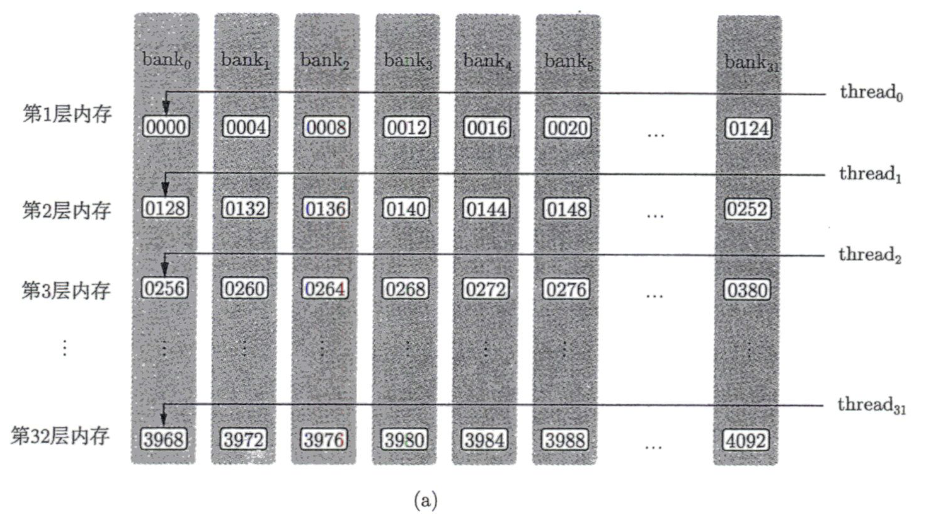
8.7 bank 的线性映射规律

当 bank 宽度为 4B 时，连续 128B = 32×4B 的共享内存内容会被均匀映射到 32 个 bank 的同一“层”：

第 1 层：bank0 拿 word0，bank1 拿 word1，… bank31 拿 word31
接下来的 128B 是第 2 层，以此类推

因此对 float s[128]：

s[0..31] → 第1层 bank0..31
s[32..63] → 第2层 bank0..31
s[64..95] → 第3层 …
s[96..127] → 第4层 …

相差 32 个 float 的元素会落在同一 bank 的不同层。

8.8 bank 冲突（bank conflict）与其在转置中的典型形态

理想情况：warp 内 32 线程访问 32 个不同 bank（或访问同一地址广播）→ 一次完成。
若多个线程访问同一 bank 的不同地址 → 发生 bank 冲突，需要拆成多次事务串行完成。

在共享内存转置中：

S 为 S[32][32]
写回阶段访问：S[threadIdx.x][threadIdx.y]
看一个 warp：常可认为 threadIdx.y = ty 固定，threadIdx.x = tx = 0..31 连续
- 访问 S[tx][ty]
- 行主序线性下标：index = tx * 32 + ty
- bank：
- 对固定 ty，warp 内 32 线程全部落在同一个 bank（bank=ty）但地址不同 → 32 路 bank 冲突（最坏情况）

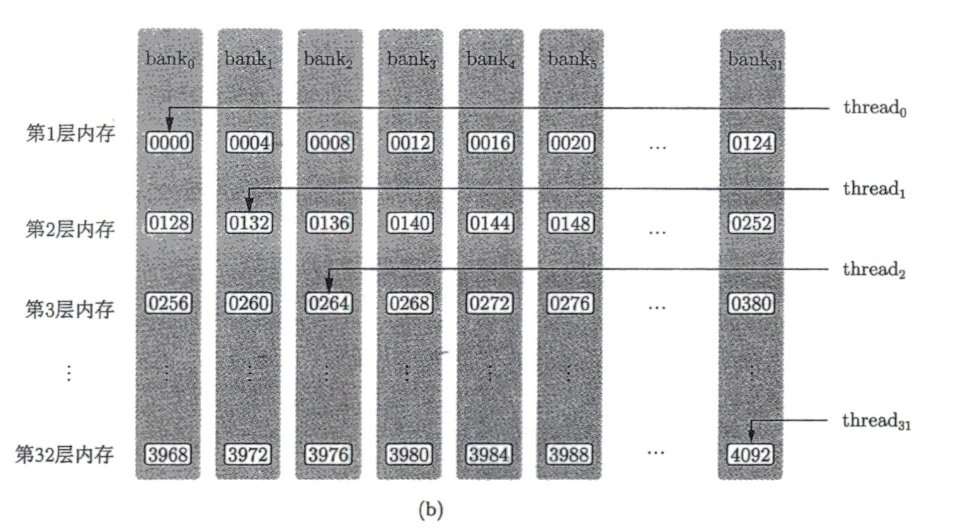
8.9 消除 bank 冲突：padding 一列（32→33）

把共享内存改为：

1	__shared__ real S[32][33]; // TILE_DIM x (TILE_DIM+1)

此时 warp 访问 S[tx][ty] 的线性下标：

index = tx * 33 + ty
bank：

当 tx=0..31 时，(tx+ty) mod 32 恰好覆盖 0..31 各不相同
→ 32 线程落在 32 个不同 bank
→ 无 bank 冲突

8.10 padding 后的性能结论与经验判断

矩阵 10000×10000（单位 ms）：

RTX 2080Ti 单精度：
- 有 bank 冲突：3.5
- padding 消冲突：2.3（明显更快，甚至快于 transpose2 的 2.8）
V100 单精度：
- 有 bank 冲突：1.8
- padding 消冲突：1.4（最好）
双精度时，“共享内存 + 消冲突”不一定最快（如 V100 双精度 2.5，transpose2 2.2 更快；2080Ti 双精度也类似）

总结判断：共享内存转置把全局读写都变为合并访问，但可能引入 bank 冲突；padding（32→33）是经典解法，可把最坏的 32 路冲突消除为无冲突，从而显著提升性能。但是否最终最优与精度、架构、缓存策略等有关，仍需实测对比。

9. 原子函数的合理使用

9.1 CUDA 原子操作（atomic operation）/ 原子函数

原子函数会对其第一个参数 address 指向的内存位置执行一次不可分割的读-改-写（read-modify-write）操作。在该事务完成前，不会被其他线程对同一地址的更新打断，从而避免并发写导致的数据竞争。

address 可以指向全局内存或共享内存。
原子更新对同一地址而言会被串行化：同一时刻对同一地址的原子操作会排队逐个完成，但不保证线程完成顺序（谁先谁后不确定）。
原子操作≠同步：原子操作只保证某个地址更新的原子性，不提供 __syncthreads() 那样的“全体线程到达屏障后再继续”的同步语义。

Pascal 架构起新增两类 atomicAdd：

atomicAdd_system()：作用范围扩展到同节点异构系统（主机 + 所有设备）。
atomicAdd_block()：作用范围限制在一个线程块内部。

原子函数的返回值语义（常见约定）：

执行前 *address 的值记为 old，执行后记为 new。
许多原子函数返回旧值 old。

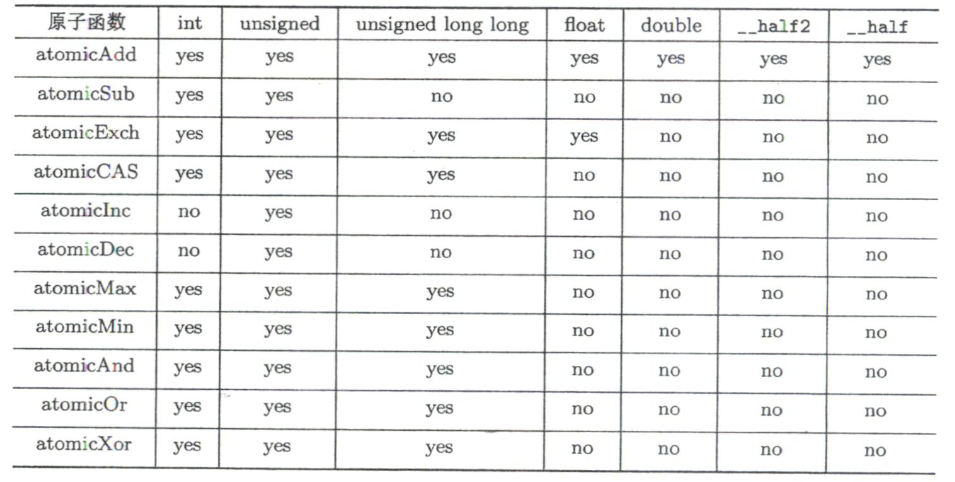
常见原子函数与更新规则：

atomicAdd(address, val)：new = old + val
atomicSub(address, val)：new = old - val
atomicExch(address, val)：new = val（交换/写入）
atomicMin(address, val)：new = min(old, val)
atomicMax(address, val)：new = max(old, val)
atomicInc(address, val)：带上限自增
new = (old >= val) ? 0 : (old + 1)
atomicDec(address, val)：带条件自减
new = ((old == 0) || (old > val)) ? val : (old - 1)
atomicCAS(address, compare, val)：比较-交换
new = (old == compare) ? val : old
atomicAnd/Or/Xor(address, val)：按位与/或/异或

类型支持：不同原子函数对 int/unsigned/unsigned long long/float/double/__half2/__half 等类型的支持不完全一致；atomicAdd()覆盖面最广。部分浮点类型（尤其 double、半精度相关）是从特定架构/计算能力起逐步支持的。

atomicCAS() 是非常“基础”的原语，理论上很多原子操作都能用 CAS 循环“软件模拟”。但当硬件已原生支持某些操作（例如新架构的 atomicAdd(double)）时，用 CAS 自己模拟通常更慢；应优先使用原生原子或从算法层面减少原子竞争。

9.2 用原子操作把归约（reduce）完全留在 GPU 上完成

原先流程：GPU kernel 只把长数组 d_x 归约成较短数组 d_y（每个 block 一个部分和），然后把 d_y 拷回主机在 CPU 上做最后求和。这样会引入额外的 Host↔Device 拷贝与 CPU后处理开销；用 nvprof 可看到 kernel 时间可能只占总时间的一部分。

目标：尽量在 GPU 上直接得到最终的一个数，从而减少拷贝与 CPU 后处理。

两种常见思路：

再启动一个/多个 kernel 继续归约，直到剩 1 个数（后文会提到两段归约的思路）。
在现有 kernel 末尾用原子加把每个 block 的部分和累加到同一位置（本节重点）。

9.2.1 为什么不能直接写 d_y[0] += s_y[0]

原先 block 内归约结束后通常写：

1	if (tid == 0) d_y[bid] = s_y[0];

如果想直接累加到 d_y[0]，直觉可能写：

1	if (tid == 0) d_y[0] += s_y[0];

但这会错，因为 d_y[0] += s_y[0] 实际是三步：

读 d_y[0]
加上 s_y[0]
写回 d_y[0]

多个 block 的 tid==0 线程会并发执行，读写会互相覆盖（race condition），导致更新丢失，结果错误。

9.2.2 正确做法：atomicAdd

改为：

1	if (tid == 0) atomicAdd(&d_y[0], s_y[0]);

要点：

atomicAdd 保证对 *address 的读-改-写是一个原子事务，避免丢更新。
顺序依然不确定，但并发意义下结果正确。
if (tid==0) 必须保留，确保每个 block 只加一次；否则一个 block 内 128 个线程都加会把结果放大 128 倍。
atomicAdd 第一个参数是指针，因此 &d_y[0] 也可写成 d_y（首地址）。
在启动 kernel 前必须把 d_y[0] 初始化为 0，否则累加基准错误。

补充实现习惯：

主机端用于 cudaMemcpy 的数组可以来自栈内存（小数据量可行），大数组不建议用栈（栈空间有限）。
“包装函数”和核函数都叫 reduce 是可行的（C++ 支持重载，只要参数列表不同）。

效果：用 “块内共享内存归约 + 块间 atomicAdd 汇总” 省掉了把部分和拷回 CPU 再求和的开销；在 RTX 2070 的测试中总时间显著缩短（文中提到比之前方案少约 2.2 ms）。

9.3 示例：邻居列表（neighbor list）的建立

问题定义：给定 𝑁 个粒子坐标，对每个粒子找出所有邻居粒子。邻居判据：两粒子距离不大于截断距离。实现中通常比较距离平方，避免每次开方（sqrt 开销大）。

该任务在分子动力学、蒙特卡洛等模拟中是常见前处理：构建邻居列表后才能做局部相互作用计算或画“键”。

9.3.1 CPU（C++）版核心思路

双重循环遍历原子对。
一旦成邻居，同时对的邻居数自增，并写入各自的邻居表。
朴素复杂度是。更高效的（如 cell list）存在，但这里为讲原理先用。

数据结构与关键参数：

输入坐标文件：xy.txt
截断距离平方：cutoff_square
每粒子最大邻居数：MN（上限过小会越界/错误；过大会浪费内存）
邻居个数数组：NN，长度 𝑁，NN[n] 表示粒子 n 的邻居数
邻居列表数组：NL，长度 𝑁 × 𝑀𝑁，NL[n*MN + k] 表示粒子 n 的第 k 个邻居编号

构建逻辑：

先把 NN 全部初始化为 0（后续要累加）。
利用对称性只算一半：只考虑 n2 > n1，如果是的邻居，则也是的邻居，可将比较次数约减半。
每次判定为邻居后做两件事（对称更新）：
1. 把写入的邻居表，并 NN[n1]++
2. 把写入的邻居表，并 NN[n2]++

关于 NN[n]++ 与 ++NN[n]：区别在表达式返回值。这里选择后缀自增是为了配合写入逻辑（先用旧值作为下标，再加 1）。

CPU 版本在测试机器上（单/双精度） find_neighbor() 计时约 250 ms。

9.4 将 CPU 邻居表构建翻译为 GPU 核函数：原子需求来自并发写

GPU 版常见做法：一个线程负责一个粒子，遍历判邻居。

如果沿用 CPU 的“对称性减半”（只算 n2 > n1，并对 n1 与 n2 两行同时写），会出现典型并发写冲突：

线程 n1 会更新 NN[n2]
线程 n2 也会更新 NN[n2]
多线程可能同时对同一个 NN[x] 做 ++（读-改-写）→ 数据竞争导致丢更新、写乱。

因此类似：

1	NL[n1*MN + NN[n1]++] = n2;

在 GPU 上若 NN[n1] 可能被多个线程更新，必须原子化。

9.4.1 容易犯的错：把原表达式拆开

直接替换成这句本身是正确的：

1	NL[n1 * MN + atomicAdd(&NN[n1], 1)] = n2;

因为 atomicAdd 返回旧值 old，这个旧值刚好就是本次写入的位置下标。

但如果拆成两句：

1 2	NL[n1 * MN + NN[n1]] = n2; atomicAdd(&NN[n1], 1);

就可能错：第一句读到的 NN[n1] 可能已经被别的线程原子更新过，读到的不再是“应该使用的旧值”。

正确写法：保存旧值再写入：

1 2	int tmp = atomicAdd(&NN[n1], 1); NL[n1*MN + tmp] = n2;

注意：即使用原子保证计数正确，邻居写入 NL 的顺序也可能每次运行不同（集合正确、数量正确，但排列不确定）。若测试/复现需要确定顺序，通常要后处理排序或设计确定性写入策略。

9.5 也可以不用原子：改变算法以避免冲突

核心思路：不再利用对称性减半；对每个 n1 遍历所有 n2（包括 n2 < n1），只往自己那一行写：

只更新 NN[n1]
只写 NL[n1*MN + …]

这样 NN[n1] 只由线程 n1 写，不会冲突 ⇒ 不需要原子。代价：计算量从“半个矩阵”回到“整个矩阵”，但避免原子开销与并发写冲突，有时反而更快、更稳定。

两个小优化点：

合并判断条件并利用短路：把更可能为假的条件放前面（例如距离判据更常失败就让它先失败）；同时排除 n2 != n1（不能把自己当邻居）。
用寄存器变量 count 暂存邻居计数，减少对全局内存 NN[n1] 的频繁读写。

还有重要内存访问优化：

将 NL 布局从 NL[n1MN + k] 改为类似 NL[kN + n1]，让 n1 连续变化时访问连续地址，更利于全局内存合并访问（coalescing）。

9.6 原子版 vs 非原子版：性能对比与结论

测试平台：GeForce RTX 2070 与 Tesla V100；分别测单精度/双精度（程序用 float 或 double）。

RTX 2070（单精度）：原子 2.5 ms；非原子 2.8 ms → 原子略快
RTX 2070（双精度）：原子 16 ms；非原子 23 ms → 原子明显更快
V100（单精度）：原子 1.8 ms；非原子 1.9 ms → 差别很小，原子略快
V100（双精度）：原子 2.6 ms；非原子 2.6 ms → 基本一样

总体结论：在这些测试中，“使用原子函数”的版本整体更好或不差，尤其在 RTX 2070 的双精度场景优势更明显；但在 V100 双精度两者几乎无差。

更重要的工程结论：算法层面的选择往往比局部 CUDA 优化更关键。低效算法再怎么调优也难以超过更高阶算法（例如的上限（除非体系非常小）。本文关注点是：在既定算法框架下写出正确且高效的 CUDA 程序，而不是系统讨论并行算法大全。

10. 线程束基本函数与协作组

10.1 GPU 层级与 SIMT 执行方式

GPU 由多个 SM（Streaming Multiprocessor）组成。
线程块（block）在运行时被调度到某个 SM 上执行：一个 block 不会被拆到多个 SM，但一个 SM 可同时驻留多个 block（取决于寄存器/共享内存等资源）。
更细粒度上，SM 以 warp（32线程）为基本调度/发射单位：warp 内线程共享同一条指令流（同一 PC），但各线程有独立寄存器上下文。
这种执行模型称为 SIMT（Single Instruction, Multiple Thread）：看起来每线程执行自己的代码，但硬件发射以 warp 为单位。

10.2 分支发散（branch divergence）

当同一 warp 内线程对同一分支 if(condition) 的判断结果不一致时：

条件为真的线程先执行分支 A，条件为假的线程在此期间闲置；
然后条件为假的线程再执行分支 B，条件为真的线程此时闲置；
→ warp 有效执行效率下降（分支两边工作量越接近、越对称，浪费越明显）。

注意区分：

不同 warp 走不同分支不叫发散（warp 本来独立调度）。
warp_id = threadIdx.x / 32：同一 warp 内 warp_id 相同，因此 switch(warp_id) 不会在 warp 内发散（最多是不同 warp 走不同 case）。
lane_id = threadIdx.x % 32：同一 warp 内 lane 不同，switch(lane_id) 会导致严重的 warp 内发散。

像 if (n < N) 的边界判断常出现在尾部不满 block/warp 的情况，通常只影响最后一部分线程，对整体性能影响有限；但不能为了避免发散而省略边界判断，否则会带来越界访问与正确性风险。

从 Volta 架构开始引入独立线程调度：warp 内推进不再满足旧架构的“锁步/天然同步”假设，因此一些依赖 warp-synchronous 的写法在 Volta+ 可能不再安全，需要更明确的同步原语（例如 __syncwarp()）。

10.3 线程束内同步：__syncwarp

在归约等场景中，如果参与线程已经落在同一个 warp（32线程）内，就不必使用 block 级同步 __syncthreads()，可改用更轻量的 warp 级同步：

1	__syncwarp(unsigned mask = 0xffffffff);

mask 是 32-bit 掩码：bit=1 的 lane 参与同步。
默认 0xffffffff 表示 32 个线程全参与。
例如 0xfffffffe 表示排除 lane 0，其余 lane 同步。

在归约中的典型策略：

当 offset >= 32（跨 warp）时：仍需 __syncthreads()。
当 offset <= 16（完全落在 warp 内）时：每轮折半后用 __syncwarp()。
这种替换可带来一定比例性能提升（文中示例约 10%），体现 warp 同步开销更低。

重要提醒：__syncwarp() 不是 __syncthreads() 的等价替换。必须保证数据依赖确实局限在同一个 warp 内，并且读写模式不会引入共享内存读写冲突。错误替换可能导致结果错误。

10.4 更常用的 warp-level primitive：vote 与 shuffle（CUDA 9+ 的 _sync 版本）

CUDA 9 起，很多线程束函数推荐使用带 mask 的 _sync 版本，以适配现代执行模型；mask 中 bit=0 的线程返回值通常“未定义”，不要依赖。

10.4.1 mask 语义

mask 是 32 位无符号整数，每位对应一个 lane（0~31）
bit=1：参与本次 warp 操作
bit=0：不参与（返回值未定义）
例如：FULL_MASK = 0xffffffff 全参与；0xfffffffe 排除 lane0

10.4.2 vote 系列

__ballot_sync(mask, predicate)：返回 32 位整数，参与 lane 中 predicate 为真则对应 bit=1（相当于由 predicate 生成新掩码）
__all_sync(mask, predicate)：参与 lane 是否全部 predicate!=0，全真返回 1，否则 0（类似 AND 归约 + 广播）
__any_sync(mask, predicate)：参与 lane 是否存在任意 predicate!=0，有则 1，否则 0（类似 OR 归约 + 广播）

10.4.3 shuffle 系列（寄存器层面跨 lane 交换数据）

__shfl_sync(mask, v, srcLane, w)：广播 srcLane 的 v 到组内所有参与 lane
__shfl_up_sync(mask, v, d, w)：lane t 取 t-d 的 v（越界返回原值 v）
__shfl_down_sync(mask, v, d, w)：lane t 取 t+d 的 v（越界返回原值 v）
__shfl_xor_sync(mask, v, laneMask, w)：lane t 取 t ^ laneMask 的 v（常用于 butterfly 结构）

参数 w（默认 32）表示把一个 warp 逻辑划分为若干宽度为 w 的小组，shuffle 只在组内发生。w 只能取 2/4/8/16/32。
当 w < 32 时，一个 warp 会被拆成多个“迷你 warp”，可用 lane_id = threadIdx.x % w（或 threadIdx.x & (w-1)）表达组内索引。

这些 _sync 函数对参与 mask 的 lane 自带隐式同步语义，因此 warp 内用它们做规约通常不需要额外 __syncwarp()；但必须使用 CUDA 9+ 的 _sync 版本。

10.5 在归约中用 shuffle 替代 “共享内存 + 条件判断 + 同步”

利用 __shfl_down_sync() 让高 lane 的值下移到低 lane，实现树形折半相加（符合归约“后半加到前半”的结构）。

关键思想：

共享内存不再必须：先把待规约值放入寄存器变量 y。

用一条语句替换 if + 同步：

1	y += __shfl_down_sync(FULL_MASK, y, offset);

替代原先：

1 2	if (tid < offset) s_y[tid] += s_y[tid + offset]; __syncwarp();

shuffle 在 warp 内以寄存器交换实现，不依赖共享内存，因此不需要为避免共享内存覆盖而写 if，也不需要显式 __syncwarp() 来隔离共享内存读写冲突。

文中测试：RTX 2070 上使用 shuffle 的归约核函数相比仅用 __syncwarp() 的版本约有 20% 性能提升；用 __shfl_xor_sync() 也可实现等价规约（本质都是 warp 内数据重排/交换）。

10.6 协作组（cooperative groups）

协作组把“线程协作”的核心能力（同步、通信/数据交换）抽象为“组”的操作，提供更统一、更可扩展的编程接口（甚至可扩展到更高层级），这里主要讲线程块级及块内再划分的小组。

使用方式：

头文件：#include <cooperative_groups.h>

命名空间：cooperative_groups
常用：

1
2
3

using namespace cooperative_groups;
// 或
namespace cg = cooperative_groups;

基本类型：thread_group 与 thread_block

thread_group：最基础的“组”抽象，常用接口：
- sync()：组内屏障同步
- size()：组大小
- thread_rank()：组内线程编号（0开始）
- is_valid()：组定义是否合法
thread_block：表示整个线程块的组：
- thread_block g = this_thread_block();
- g.sync() 约等价于 __syncthreads()
- group_index()≈blockIdx，thread_index()≈threadIdx

tiled_partition()：把线程块划分为多个固定大小的“片”（tile），片大小必须是 2 的幂且 ≤ 32：2/4/8/16/32。

例如把 block 划成若干 32 线程片（warp规模）：

1	thread_group g32 = tiled_partition(this_thread_block(), 32);

还可继续细分，例如把 32 线程片再切成 4 线程片。

模板化版本（编译期固定大小，通常更高效）：

1 2	thread_block_tile<32> g32 = tiled_partition<32>(this_thread_block()); thread_block_tile<4> g4 = tiled_partition<4>(this_thread_block());

thread_block_tile 提供类似 warp intrinsics 的接口（不需要 mask 参数，tile 内默认全参与；也不需要 w 参数，因为 tile 大小已固定），包括 ballot/all/any/shuffle 等。如：

unsigned __ballot_sync(int predicate);
int      __all_sync(int predicate);
int      __any_sync(int predicate);

T __shfl_sync     (T v, int srcLane);
T __shfl_up_sync  (T v, unsigned d);
T __shfl_down_sync(T v, unsigned d);
T __shfl_xor_sync (T v, int laneMask);

结论：用协作组改写归约，性能与直接用 warp shuffle 基本等价（底层走同样硬件路径），但协作组更统一、更易扩展到“非整 warp 的小组协作”。

10.7 提高线程利用率：先“多算一点”再归约

以 BLOCK_SIZE=128 的树形归约为例，offset 折半：64、32、…、1：

offset=64：只有 1/2 线程工作
offset=32：只有 1/4 线程工作
…
offset=1：只剩 1/128 线程工作

共 log2(128)=7 步，平均利用率约 (1/2+1/4+…)/7≈1/7，归约阶段大量线程闲置。

优化思路：进入共享内存归约前，让每个线程先在寄存器里对多个全局内存元素做累加，使归约前的循环阶段线程利用率接近 100%。

为保持合并访问，不让同一线程处理“相邻的多个元素”（会破坏合并），而使用 grid-stride：

相邻线程仍访问相邻地址（保持合并）
同一线程跨迭代访问的元素之间相隔 stride

结果汇总策略：不再依赖 atomicAdd。改为两段式：

第 1 次 kernel：每个 block 得到一个部分和写入 d_y[bid]
第 2 次 kernel：再把 d_y 归约成最终结果

这样在不使用原子操作的情况下得到最终和，并且树形归约的加法结构更稳定。

性能与精度（RTX 2070 单精度示例）：

总时间约 2.0 ms，相比之前最优版本再提升约 40%
精度：结果约 123000064.0，相对精确值 123000000.0 有约 7 位有效数字
之前原子累加的结果 123633392.0 只有约 3 位有效数字（原子累加顺序不确定导致数值不稳定）

10.8 避免反复 cudaMalloc/cudaFree：用静态全局设备变量替代中间缓冲区

在 reduce() 包装函数中，为中间数组 d_y 反复 cudaMalloc/cudaFree 会显著拖慢整体，因为设备端动态分配/释放开销很大。

优化：把中间缓冲区改为编译期静态分配：

1	__device__ real static_y[GRID_SIZE];

如果不想改核函数形参，也可以在主机端用 cudaGetSymbolAddress() 拿到该静态变量的设备地址指针，当作普通 d_y 传入：

1	cudaError_t cudaGetSymbolAddress(void *devPtr, const void symbol);

symbol 可以是 __ device__ 或 __ constant__ 变量名。

效果：仅替换为静态全局内存后，总时间可从约 2.0 ms 降到 1.5 ms（单精度示例），说明动态分配确实是瓶颈之一；工程上也应尽量避免在内层循环里反复做 cudaMalloc/cudaFree。

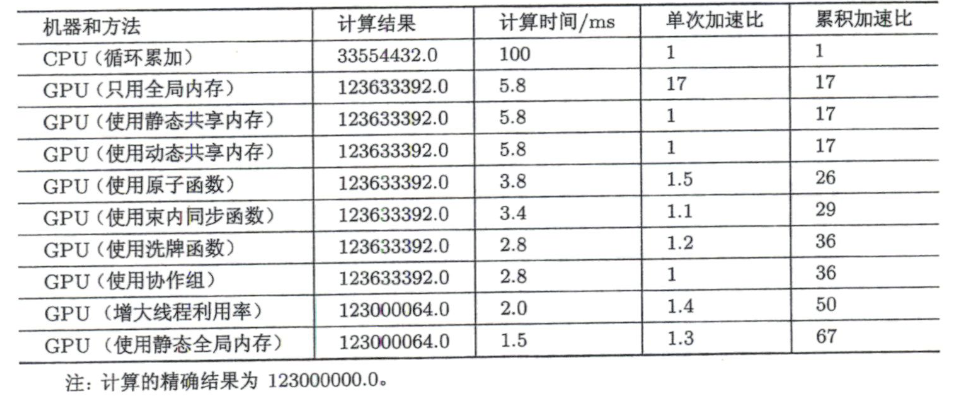
归约全过程对比：

CPU（循环累加）：100 ms，结果 33554432.0
GPU（只用全局内存/静态共享/动态共享）：5.8 ms，结果 123633392.0
GPU（原子函数）：3.8 ms
GPU（束内同步 __syncwarp）：3.4 ms
GPU（洗牌/协作组）：2.8 ms
GPU（增大线程利用率）：2.0 ms，结果 123000064.0
GPU（使用静态全局内存）：1.5 ms，结果 123000064.0

11. CUDA流

11.1 CUDA 程序的“两层并行”

核函数内部并行：线程/warp/block 的并行组织与执行。
核函数外部并行（更宏观）：包括但不限于
1. 核函数计算与数据传输的并行
2. 主机计算与数据传输的并行
3. 不同数据传输之间的并行（取决于 memcpy 方向/类型、是否异步等）
4. 核函数计算与主机计算的并行
5. 不同核函数之间的并行

通常加速的第一优先仍是：尽量让计算留在设备端、减少 Host↔Device 传输。但很多应用里核外并行仍很关键，引出 CUDA stream。

11.2 CUDA 流（stream）的定义与基本 API

一个 CUDA 流可理解为：主机发出的、在设备上执行的一串 CUDA 操作序列（包含 H↔D 拷贝、kernel launch 等）。

同一流内：按发布顺序依次执行（顺序性）。
不同流之间：可能并发/交错执行（并行来源）。
任意 CUDA 操作都属于某条流：默认流（default/null stream）或显式创建的非默认流。

创建/销毁：

cudaStreamCreate(cudaStream_t*)
cudaStreamDestroy(cudaStream_t)

检查流是否完成：

cudaStreamSynchronize(stream)：阻塞主机，直到该流内所有操作完成
cudaStreamQuery(stream)：不阻塞；完成返回 cudaSuccess，否则返回 cudaErrorNotReady

11.3 默认流下的“主机计算 vs 设备计算”重叠

典型默认流顺序：

cudaMemcpy(H→D)：x
cudaMemcpy(H→D)：y
sum<<<…>>>(…)
cudaMemcpy(D→H)：z

设备视角：默认流严格按代码顺序排队执行。
主机视角：

cudaMemcpy 是同步/阻塞：调用后主机等待完成才能继续。
kernel launch 异步/非阻塞：launch 后主机立即拿回控制权。
但紧接着的 cudaMemcpy(D→H) 会由于默认流顺序性而等待 kernel 完成，同时主机也会被这次 memcpy 阻塞。

因此一种常见重叠方式：把主机计算放在 kernel launch 之后、下一次会阻塞的操作之前，实现 CPU 与 GPU 并行。

结论：

当主机函数与设备核函数耗时相近，把主机计算放到 kernel launch 之后可显著降低总时间（接近 2× 潜在收益）。
若主机远慢于 GPU：主机瓶颈，收益有限。
若主机远快于 GPU：GPU瓶颈，主机时间本来占比小，收益也有限。

11.4 多流实现“多个核函数之间并行”

同一流内核函数顺序执行，无法重叠。要并发/交错执行多个 kernel，必须放到不同 stream。

核函数 launch 三种写法（第三种显式指定 stream）：

my_kernel<<<N_grid, N_block>>>(args);
my_kernel<<<N_grid, N_block, N_shared>>>(args);
my_kernel<<<N_grid, N_block, N_shared, stream_id>>>(args);

参数含义：

N_grid：网格大小
N_block：线程块大小
N_shared：动态共享内存字节数
stream_id：流句柄

注意：使用非默认流时必须用四参数形式；即使不需要动态共享内存，也要写 0：

1	my_kernel<<<N_grid, N_block, 0, stream_id>>>(args);

不能把 stream_id 误写到第三个位置。

实践：创建若干非默认流 streams[]，在不同流中启动相同 kernel（每个 kernel 处理不同数据段）。实验（Tesla K40）显示：随着流数增加，并发核函数数量上升，总时间不会按任务量同比例增长，相对单流顺序执行出现明显加速；多流可减少 SM 闲置，提高整体利用率。

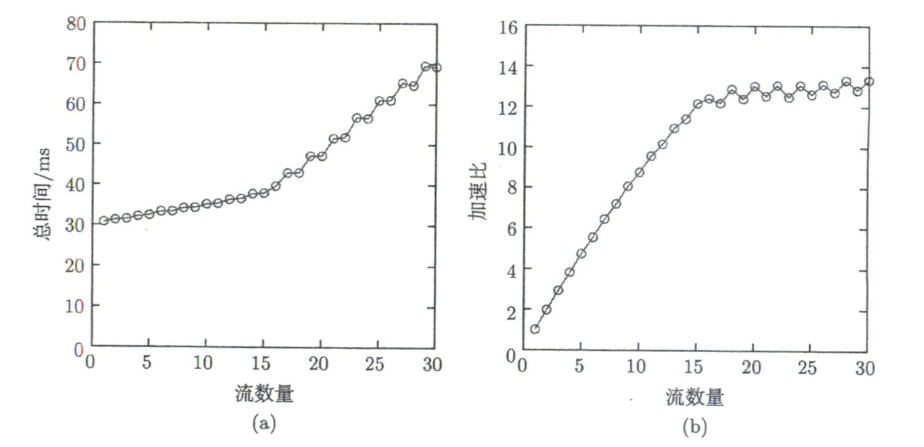
并发天花板来自两类限制：

计算资源上限（SM/寄存器/共享内存等）
单 GPU 可并发执行的 kernel 数上限（随架构变化）

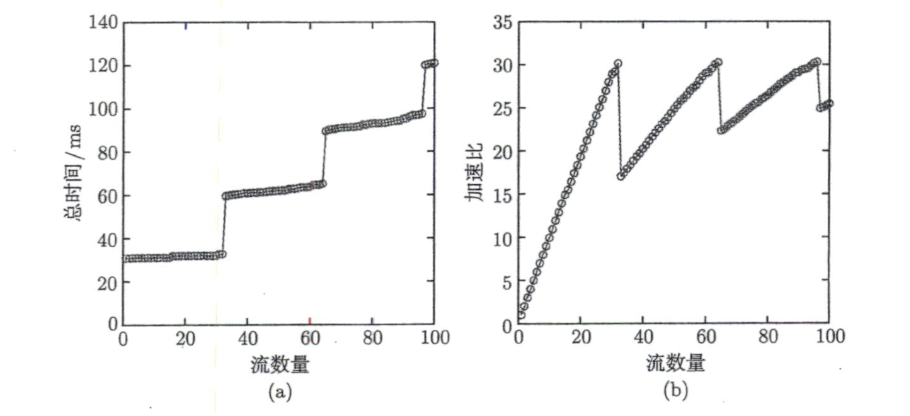
性能通常在某个流数附近最好（如 32），再增大流数反而可能变慢（调度与额外开销 + 并发上限共同作用）；换不同架构（P100/V100等）曲线与最优流数可能不同。

11.5 让“核函数执行”与“数据传输”真正重叠：异步拷贝 + pinned 内存 + 分块流水线

要做到 H2D/KER/D2H 真重叠，关键是：

使用非默认流
使用 cudaMemcpyAsync(…, stream)
主机内存必须是 pinned（不可分页）

11.5.1 为什么必须是异步拷贝

若用同步 cudaMemcpy：主机发出拷贝命令后会阻塞，无法继续往其他流提交 kernel 或其他操作，谈不上重叠。

cudaMemcpyAsync 比 cudaMemcpy 多了 cudaStream_t stream 参数，可将拷贝排到指定流中，拷贝由 DMA 执行，主机可继续提交其他工作。

11.5.2 为什么主机内存必须 pinned

pageable 内存：OS 可能换页/移动物理页，GPU DMA 无法直接稳定访问。
若把 pageable 内存交给 cudaMemcpyAsync，常会退化：先拷到临时 pinned 区再 DMA → 主机端行为变同步/阻塞，破坏重叠；甚至出现“流越多越慢”。

pinned 内存分配：

cudaMallocHost(void** ptr, size_t size)
cudaHostAlloc(void** ptr, size_t size, size_t flags)（默认 cudaHostAllocDefault 效果等价；注意没有字母 M）

释放必须用：

cudaFreeHost(ptr)
误用 free() 会出错。

11.6 分块流水线（pipeline）

将一次完整流程抽象为三段：

H2D：Host → Device
KER：kernel
D2H：Device → Host

单默认流严格串行：H2D → KER → D2H。

即使把三段放三个流，但若对同一份数据仍有严格依赖，也不会自动加速。要依赖多流加速，需把数据切成 num 份，每个流处理一份：

Stream i：H2D(i) → KER(i) → D2H(i)

不同流之间形成流水线重叠：

Stream1 做 KER 时，Stream2 可做 H2D
Stream1 做 D2H 时，Stream2 可做 KER
理想最大加速上限约 3（H2D/KER/D2H 三段完全叠满）。

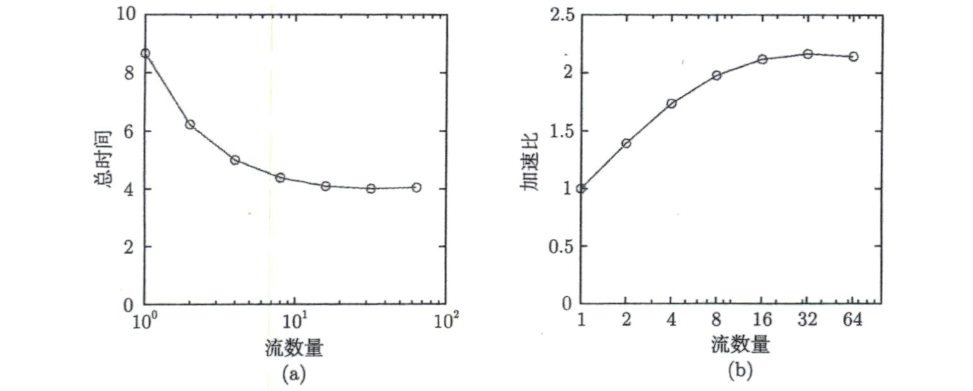
示例：32 个流获得约 2× 加速（未达 3×），主要原因：

三段时间不完全相等，流水线叠不满
每个流的第一个操作都是 H2D，H2D 之间无法无限并行（硬件限制）
流数太多会带来额外开销（更多 launch、排队调度），超过某点加速比下降

工具上可用 nvvp 等观察时间线（不展开）。

12. 使用统一内存编程

12.1 统一内存（Unified Memory）的概念与优缺点

统一内存提供一种逻辑上的共享地址空间：CPU/GPU 都能用同一个指针访问同一份数据，省去手动 H2D/D2H 拷贝与双指针管理。写 CUDA 不强制使用统一内存。

实现依赖 CPU/GPU 内存管理单元协同实现一致性与迁移；较新架构（文中提到帕斯卡后能力更强，关键在更完善的缺页/异常处理）统一内存体验与性能更好；老架构能力相对弱。更高级的 UM 特性往往要求更高架构 + Linux；在一些特定硬件平台（如 Power9 + NVLink）还可能具备更强的“设备访问主机内存”能力，但普通用户不一定具备。

主要优势：

编程简单：无需显式 cudaMemcpy，无需 host/device 两份内存管理。
可能更好性能：系统/驱动可自动将数据迁移到更靠近计算发生处（策略得当时）。
支持 oversubscription：显存不够时数据可在主机内存与显存间按需迁移/换页（但会引入缺页与迁移开销）。

基本用法：

在主机端用 cudaMallocManaged(…) 分配统一内存，用 cudaFree(…) 释放。
kernel 内访问与普通 global memory 写法几乎一致：同一指针 CPU/GPU 都能用。
统一内存可以与非统一内存混用；老代码可逐步迁移，不必一步到位。
静态统一内存：全局变量加 __ managed__（常见写法 __ device__ __ managed__ …）可定义静态 UM 变量。

12.2 统一内存的“超量分配”与 touch 行为

对比现象：

不用 UM（cudaMalloc）：接近显存上限即失败（例如到 ~7GB 再分配报 OOM）。
用 UM（cudaMallocManaged）但“不触碰”内存：看起来可分配很大（如 30GB）而不报错。原因：更多是预留地址空间/建立映射，不等价于立刻占用物理内存/显存；真正分配/迁移往往在第一次访问（touch）时发生。
GPU 侧 touch（在 GPU 上初始化/写入）会触发真实驻留与迁移：受限于“显存 + 主机内存可用量（扣除系统与其他进程占用）”，触碰到某阈值后可能失败（如触到 ~20GB 后失败，或出现非法访问等）。
仅 CPU 侧 touch 不等价于“把 GPU 显存也用上”：只在 CPU 访问时更可能主要消耗主机内存；主机内存吃紧进程可能被系统杀掉（出现 “Killed”）。要把主机与设备两侧资源更有效纳入 UM 池子，需要让 GPU 参与访问/迁移或使用预取等机制。

12.3 让统一内存更快：减少缺页与抖动迁移（hints）

UM 高性能关键：减少 page fault，保持局部性，避免 CPU/GPU 之间频繁抖动迁移。可用 API 给运行时提示：

cudaMemPrefetchAsync(…)：在某 stream 中把一段 UM 预取/迁移到指定设备（或迁回主机），减少运行时缺页与随机迁移开销
cudaMemAdvise(…)

原则：能预取尽量预取，用主动迁移换更可控的访问行为；整体仍比手写大量显式拷贝省心，但性能上需要“配合”运行时。

13. CUDA标准库的使用

13.1 CUDA 库概览与价值

CUDA 工具链除数学函数外还提供大量高性能库，覆盖线性代数、FFT、稀疏计算、随机数、深度学习等，例如：

Thrust、cuBLAS、cuFFT、cuSPARSE、cuRAND、cuSolver、cuDNN 等

使用库的主要好处：

节省开发时间（许多功能自研成本高）
可靠性更高（长期打磨）
简化代码（复杂功能往往从上百行降到几十行调用）
可能更快（但某些特定问题自写 kernel 仍可能更合适，库调用也可能受访存/调度等因素影响）

13.2 Thrust：CUDA 版“STL 风格”并行算法库

Thrust 是 C++ 模板库，风格类似 STL，通过 thrust:: 命名空间避免与 std:: 冲突（如 thrust::sort vs std::sort）。

数据结构：

thrust::host_vector：主机端向量
thrust::device_vector：设备端向量
使用时包含对应头文件（如 thrust/host_vector.h、thrust/device_vector.h）。

常用算法类别：

transformation（变换）
reduction（归约）
prefix sum/scan（前缀和/扫描）
sorting/searching（排序/搜索）
reordering（选择性复制、替换、移除、分区等重排）

13.3 前缀和（prefix sum）/ 扫描（scan）

定义：

inclusive scan：
exclusive scan：

使用 thrust::inclusive_scan() 的思路：传迭代器（或设备指针 + execution policy）对设备数据做扫描。

选择建议：

如果程序大量用 Thrust：device_vector 更合适（生态一致）。
如果主要自写 kernel、偶尔用 Thrust：用设备指针更直接（更底层、接近原生 CUDA）。

13.4 cuBLAS：CUDA 版 BLAS

BLAS 起源于 Fortran 生态，因此 cuBLAS 强烈体现列主序（column-major）传统，这是使用 cuBLAS 最关键的约束/坑点。

API 分类：

cuBLAS API：数据在设备端
cuBLASXT API：数据在主机端
cuBLASLt API：更偏矩阵乘法专用（CUDA 10.1 引入）

这里重点介绍 cuBLAS API。

矩阵乘法（GEMM）：

编译链接：-lcublas
头文件建议用新版：<cublas_v2.h>（旧 <cublas.h> 不建议）

关键流程：

主机端准备矩阵（一维数组表示），注意列主序存储约定
cublasSetVector()：把主机数组拷到设备数组（理解 incx/incy：跨步拷贝）
创建/销毁句柄：cublasCreate() / cublasDestroy()
调 cublasDgemm() 做乘法：
计算，
其中 transa/transb（不转置/转置/共轭转置），以及 lda/ldb/ldc（leading dimension；列主序下通常对应“行数”）
cublasGetVector() 把结果从设备拷回主机并输出（输出仍需按列主序理解）

13.5 cuSolver：更高层线性代数（类似 LAPACK）

cuSolver 做更高级线代（矩阵求逆、特征值/向量、分解等），实现上依赖 cuBLAS + cuSPARSE，定位类似 Fortran 体系的 LAPACK。

子库划分：

cuSolverDN：稠密矩阵
cuSolverSP：稀疏矩阵
cuSolverRF：稀疏矩阵分解的 Refactorization

cuSolver 调用倾向异步执行；若需确保完成可用 cudaDeviceSynchronize()。设备端执行的 cuSolver 调用要求数据已在设备端准备好，H↔D 传输由用户负责。

例：厄密矩阵本征值（2×2 厄密矩阵）

cusolverDnZheevd_bufferSize() 先算工作区大小
分配工作区
cusolverDnZheevd() 求本征值（jobz 控制是否求本征向量）

命名解释：

Z：双精度复数（cuDoubleComplex，别名 double2）
he：Hermitian
evd：divide and conquer 求本征值/向量
对比：evj（Jacobi）、gvd（广义本征值）等。

13.6 cuRAND：随机数生成库

区分伪随机（pseudo-random）与准随机（quasi-random），此处只关注伪随机。cuRAND 提供主机 API 与设备 API，这里只介绍主机 API。

主机 API 标准流程：

定义生成器句柄：curandGenerator_t generator
curandCreateGenerator(&generator, rng_type)：选择 RNG 算法
- CURAND_RNG_PSEUDO_XORWOW（默认/常用）
- CURAND_RNG_PSEUDO_MT19937（质量可能更高但更耗时/更耗资源）
设定 seed：curandSetPseudoRandomGeneratorSeed(generator, seed)（同种子产生同序列）
生成随机数到设备数组：
- 均匀分布（double）：
  curandGenerateUniformDouble(generator, g_x, N)
- 正态分布（double）：
  curandGenerateNormalDouble(generator, g_x, N, mean, stddev)
用完销毁：curandDestroyGenerator(generator)